ここでは、基本的な3つの図形の断面2次モーメントを求めながら、計算方法を覚えていきましょう。
四角形の断面2次モーメント
以下の図で考えてみます。
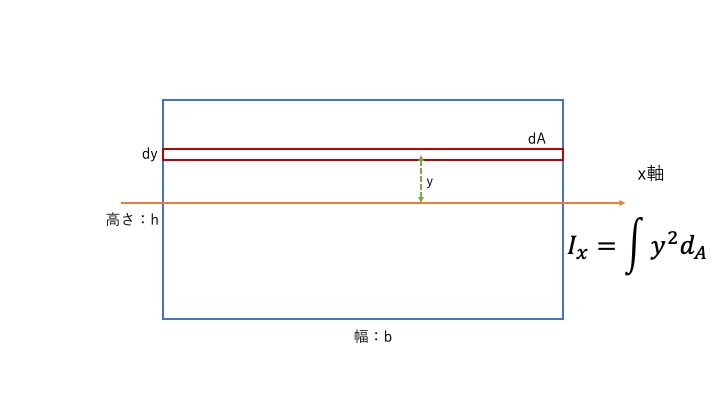
四角形の真ん中をx軸が通っているとします。
X軸に対して、断面2次モーメントを求めてみましょう。

このように四角形の断面2次モーメントが求められました。
三角形の断面2次モーメント
三角形も同じです。以下の図で考えてみましょう。
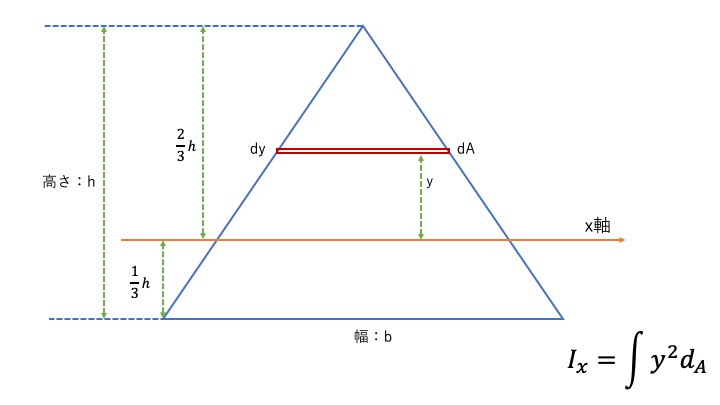
この場合のdAはy軸からの距離によって面積が変わりますね。
ここに注意して解いてみましょう。

円の断面2次モーメント
円は少し複雑です。以下の図で考えてみましょう。
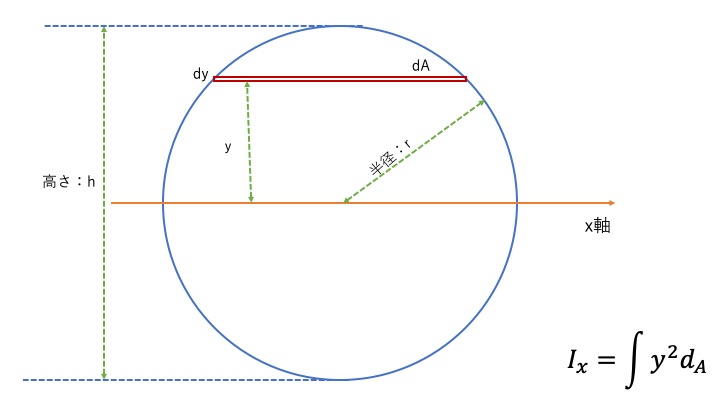
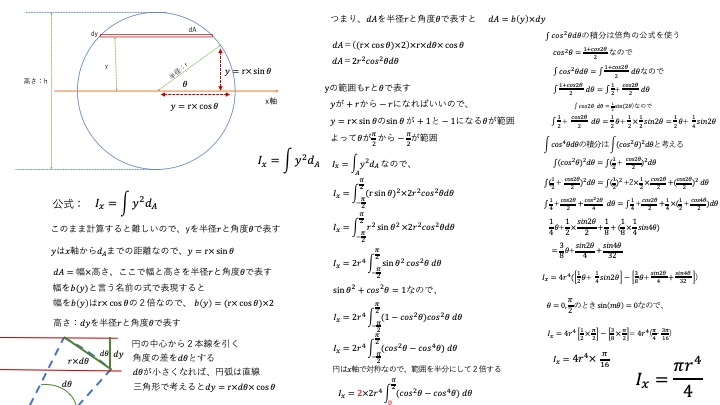
この場合、そのまま計算するとややこしいので、yを半径rと三角関数を使って表します。
x軸に対する断面2次モーメントが分かれば、底辺と高さを入れ替えて覚えよう
ここまで、x軸に対する断面2次モーメントを計算してきました。
y軸に対する断面2次モーメントは高さと幅を入れ替えましょう。
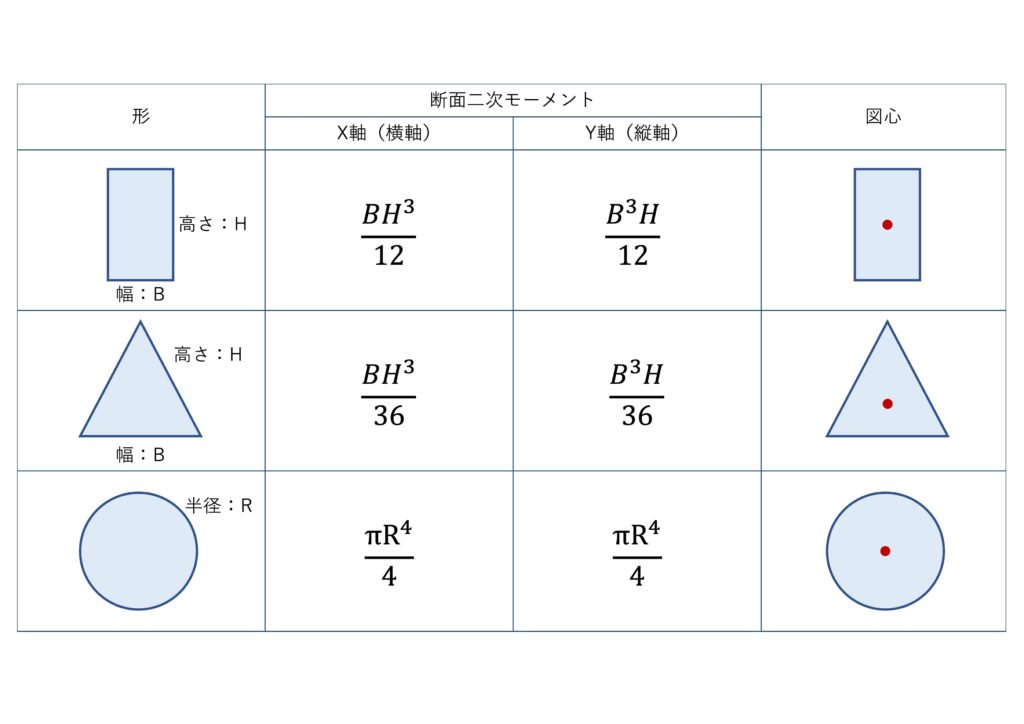
では、一覧表を出しておきます。必要な時に見れるように保存しておいてくださいね。
平行軸の定理の導出
【公式】
以下の例を計算してみましょう。

つまり、図心からずれた断面2次モーメントは以下の式で計算できます。
(図心を通る断面2次モーメントの2乗)+(図心からのずれの2乗×面積)
【参考】図心の求め方
図心の求め方は断面1次モーメントを使います。
つまり、断面1次モーメントを面積で割ったものが図心の位置になります。
図心の求め方や断面1次モーメントについては、『【断面一次モーメントとは】公式と図心の求め方をわかりやすく解説します』で詳しく解説しています。
