
「断面二次モーメントって、結局何?」
「断面一次モーメントと何が違うの?」
「単位が\(m^{4}\)なのはなぜ? 」
構造力学を学び始めた学生の皆さんは、まずこの定義の段階でつまずくことが多いです。
私(明石高専卒)も、最初は物理的な意味が理解できず、公式を丸暗記してテスト対策をしていました。
しかし、基礎を正しく理解すれば、複雑な計算もスムーズに進みます。
この記事は、「断面二次モーメントが全くわからない」という初学者のために、その意味、単位、そして基本公式を最も分かりやすく解説します。これを読めば、次に進むべき『断面二次モーメントの計算方法 』に迷わず進めるはずです。
目次
断面二次モーメントとは?結論は「梁の曲がりにくさ」を示す指標

断面二次モーメントとは、結論から言うと「部材の曲がりにくさ」を示す指標です。
構造物に使われる柱や梁(はり)などの部材は、力を受けると曲がろうとします。
この時、「材料の強さ」(ヤング率など)ではなく、その部材の「断面の形と大きさ」だけで決まる、曲げに対する抵抗力こそが「断面二次モーメント」なのです。
断面二次モーメントのわかりやすいイメージ

定規で想像して見ましょう。
- 定規を「横向き」(平たい状態)にして曲げてみると、どうでしょう?少し力を入れただけで、簡単にグニャリと曲がってしまいます。
- 次に、その定規を「縦向き」(立てた状態)にして曲げてみてください。先ほどと同じ力を加えても、ほとんど曲がらないはずです。
これが、断面二次モーメントの働きを最もよく表す現象です。使う材料や面積は全く同じなのに、「力の方向に対する断面積の配置」を変えるだけで、曲がりにくさ(抵抗力)が劇的に変わるのです。
つまり、断面二次モーメントは、曲げモーメントが作用した際に、断面内の面積を軸から遠い位置に配置するほど、大きくなります。
なぜ「モーメント」なのか?定義の基本的な考え方
なぜ「断面二次モーメント」という、少し大袈裟な名前がついているのでしょうか。分解して考えてみましょう。
- モーメント(Moment):「回転させようとする力」や「影響力」を意味します。テコの原理で、作用点から遠いほど小さな力で大きな影響が出るように、軸から遠いほど影響が大きいという概念です。
- 二次:力学では、距離の2乗をかけた影響力を指します。
曲げモーメントが梁に作用した際、抵抗力(断面二次モーメント)は、中立軸(回転の中心)から断面積が遠いほど、抵抗力を強く発揮します。
この抵抗力の影響度を測る計算式が、「断面積 \( \times \) 軸からの距離の2乗」という形になっており、この「距離の2乗」があるからこそ「二次」モーメントと呼ばれているのです。
断面二次モーメントの定義式と単位を理解しよう

前のセクションで、断面二次モーメントは「曲がりにくさ」を示す指標であり、「断面積の軸からの距離の2乗」に比例することが分かりました。これを数学的に表現したものが「定義式」です。
\( I = \int y^{2} dA \)
一見複雑な積分記号 \(\int \)が出てきますが、今は深く考えなくて大丈夫です。この式は、単純に断面積(\(dA\))と、回転の中心軸からの距離の2乗(\(y^{2}\))を、断面全体でひたすら足し合わせている(積分している)ことを示しています。
断面二次モーメントの単位はなぜ長さの4乗 \(m^{4}\) なのか?
断面二次モーメントは、なぜ「長さの4乗」という直感的ではない単位になるのでしょうか?
それは、定義式を構成する要素の単位が以下のように組み合わされているからです。
| 要素 | 意味 | 単位 |
|---|---|---|
| \(dA\) | 微小な断面積 | \(m^{2}\)(長さの2乗) |
| \(y^{2}\) | 軸からの距離の2乗 | \(m^{2}\)(長さの2乗) |
| \(I\) | 断面二次モーメント | \(m^{2} \times m^{2}\)(長さの4乗) |
つまり、「面積」を構成する長さの2乗と、「距離の2乗」を掛け合わせるため、結果として長さの4乗という単位になるのです。この単位は、断面二次モーメントが「断面積の、軸からの影響度」を表していることを示しています。
断面二次モーメントの定義式(積分)を図でわかりやすく解説
定義式自体を深く理解したい読者のために、積分がどのように行われているのかを図で視覚的に解説します。
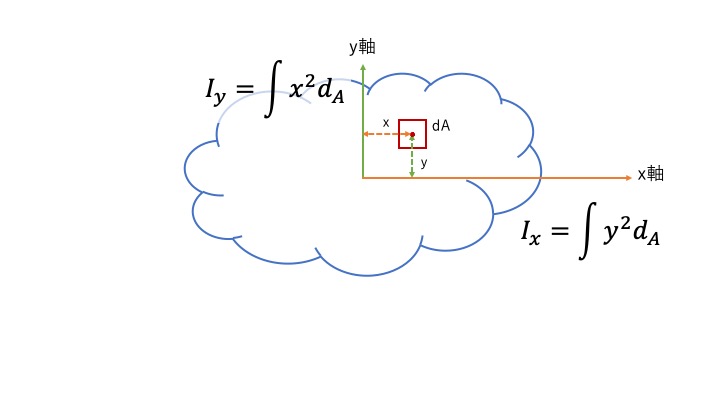
- \(y\):回転の中心(中立軸)からの垂直距離
- \(dA\):断面内のごく小さな面積
- \(y^{2}dA\):断面二次モーメント
この積分の具体的な計算方法(導出)については、断面二次モーメントの「求め方」完全講義で、長方形や円形などの具体的な図形を例に徹底解説しています。計算手順を学びたい方は、ぜひこちらの記事をご覧ください。

断面二次モーメントと断面一次モーメントや断面係数の違い

多くの人が混同しやすい断面二次モーメントと断面一次モーメント、断面係数との違いを解説します。
断面二次モーメントと「断面係数」の決定的な違い(応力との関係)
断面二次モーメント\(I\)を理解できたら、次に必ずセットで出てくるのが断面係数\(Z\))です。学生の多くは「どちらも断面の曲げに対する強さだろう」と混同しがちですが、これらには構造計算上、決定的な役割の違いがあります。
| 項目 | 断面二次モーメント | 断面係数 |
|---|---|---|
| 物理的な意味 | 曲がりにくさ(たわみにくさ) | 強さ(応力の発生しにくさ) |
| 計算式 | \( I = \int y^{2}dA \) | \(Z = I / y_{max}\)(最大応力距離で割り算) |
| 利用する場面 | はりのたわみ(変位)の計算 | はりの応力の計算 |
| 求めたいこと | 部材がどれだけ変形しにくいか | 部材がどれだけ破壊されにくいか |
最も重要な違いは、「断面二次モーメントは変形(たわみ)に関係し、断面係数は応力(破壊)に関係する」という点です。
例えば、梁のたわみ量を求める公式には$I$が使われ、梁の最大曲げ応力\(\sigma\) を求める公式には \(Z\) が使われます。
\(\sigma = \frac{M}{Z} \)(最大応力)
この公式を見ればわかる通り、断面係数 \(Z\) が大きいほど、発生する応力 \(\sigma\) は小さくなります。つまり、断面係数は「部材が破壊される強さ」を示す指標なのです。
断面一次モーメントとの違いと「図心(重心)」の関係
もう一つ、「断面一次モーメント」という概念もあります。断面一次モーメントは、断面二次モーメントの定義式で\(y\)が1乗になっているものです。
| 項目 | 断面一次モーメント | 断面二次モーメント |
|---|---|---|
| 定義式 | \( S = \int y dA \) | \(I = \int y^{2} dA\) |
| 役割 | 図心(重心)の位置を求める | 剛性(曲げにくさ)を示す |
| 単位 | 距離の1乗 | 距離の2乗 |
筆者は構造力学が苦手だった頃、この2つをよく混同しましたが、「一次は図心探し、二次は曲げ対策」と目的を割り切って覚えることで混乱を避けました。計算の際は、「二次には距離の \(y^2\) がつく」と覚えておけば間違いありません。
「断面一次モーメントの定義をもっと深く知りたい」「図心(重心)の求め方を詳しく学びたい」という方は、こちらの『【断面一次モーメントの計算方法】意味・図心の求め方をわかりやすく解説』で徹底的に解説しています。

断面二次モーメントの実際の「働き」を知る

構造力学を少しでも勉強すると、梁や柱には「H形鋼」や「I形鋼」といった独特な断面の鋼材が使われていることに気づきます。なぜ、わざわざ複雑な形にするのでしょうか?
その答えこそが、「断面二次モーメントを最大化するため」です。
I形鋼やH形鋼はなぜ強い?形状と曲がりにくさの関係
H形鋼やI形鋼は、断面積の大部分を、中立軸から最も遠い上下のフランジ(つば)に集中させています。
前述の通り、断面二次モーメントの抵抗力は距離の2乗で効いてくるため、
- 断面積を中立軸から遠くに配置するほど、Iの値は劇的に大きくなります。
- 逆に、中立軸付近にあるウェブ(腹板)の断面積は、Iへの貢献度は小さいです。
つまり、H形鋼の形は、部材の「強さ」と「軽さ(経済性)」を両立させるために、最も効率よく曲がりにくさ(断面二次モーメント)を稼げるように設計された、力学的な究極の合理的な形なのです。
断面二次モーメントをどう使うか?
断面二次モーメントは、特に以下の二つの重要な実務シーンで不可欠な知識となります。
たわみ量の計算
構造設計において、梁や床が許容範囲を超えてたわむと、建物や橋梁の機能に支障をきたします。このたわみ量を計算するために、断面二次モーメント\(I\)は必ず使用されます。設計者は、この\(I\)を大きくするために、梁の高さを高くするといった断面計画を行います。
部材選定とコスト管理
部材が強くなるからといって、無闇に大きな断面の部材を使うと、コストと重量が増大します。現職で材料メーカーにいる私自身の経験からも言えますが、設計部門では常に、必要な強度と剛性\(I\)を満たしつつ、最も経済的で施工性の高い部材を選定する必要があります。断面二次モーメントの知識は、この合理的な判断の根拠となるのです。
次のステップ:断面二次モーメントの「求め方」をマスターしよう
ここまでで、断面二次モーメントが「曲がりにくさ」の指標であることが深く理解できたはずです。次に、構造力学の試験や設計で不可欠となる「計算」のステップに進みましょう。
【導入】 断面二次モーメントの長方形の公式を確認
最も基本となる長方形断面の断面二次モーメントは、中立軸(図心)に対して以下の公式で求められます。
\( I = \frac{bh^3}{12}\)
この公式こそ、高さ(\(h\))が3乗で効いてくることを示しており、「高さ方向に部材を立てるほど、曲がりにくさ(\(I\))が劇的に向上する」という、前項で解説した物理的な意味を裏付けています。
【重要】複雑な形状の計算に必須な「平行軸の定理」とは
しかし、実際の構造部材は単純な長方形ばかりではありません。L字形、T字形、さらに複雑な合成断面も多く使われます。これらの断面の\(I\)を求めるために、「平行軸の定理」という非常に重要な計算ルールを使います。
平行軸の定理を使うことで、複雑な図形も、複数の単純な図形に分割し、それぞれの\(I\)を足し合わせることで求めることができるようになります。
詳細な計算と例題はこちらの記事で解説!
断面二次モーメントの「公式の導出」「長方形以外の図形の求め方」「平行軸の定理を使った具体的な例題」など、計算の全ステップについては、こちらの記事で徹底的に解説しています。
【こちらをクリック】 断面二次モーメントの求め方:公式の導出から例題まで徹底解説!
の理解が深まった今こそ、計算力をマスターする絶好の機会です。次のステップへ進みましょう。
まとめ:断面二次モーメントは「梁の性能」を知る最も重要な指標
この記事では、あなたがこれまで公式の暗記で終わらせていたかもしれない「断面二次モーメント」について、以下の3点を中心に解説しました。
- 断面二次モーメントとは: 部材の「曲がりにくさ」(たわみにくさ)を示す、断面の形と大きさで決まる指標
- 単位: 「\(m^{4}\)(長さの4乗)」で、断面積 \(\times \) 距離の2乗 の積算で求める
- 他との違い: 「断面係数」は破壊に対する強さ、「断面一次モーメント」は図心を求めるための指標
構造力学の土台となるこの概念の理解は、あなたの学生生活やエンジニアとしてのキャリアを大きく助けるはずです。ぜひ、この知識を基に次のステップ(計算)へと進み、断面二次モーメントを完全にマスターしてください。
【次のステップへ】断面二次モーメントの求め方もマスターしよう!
断面二次モーメントの「曲がりにくさ」という物理的な意味が理解できれば、構造力学はもう怖くありません。知識を定着させ、試験や実務で使える武器にするため、次のステップへ進みましょう。
1. 最重要:計算力をマスターし、構造力学の試験を突破する
概念の理解の次は、具体的な「計算」のステップです。長方形からT形、I形、そして複雑な合成断面まで、あらゆる図形の断面二次モーメントの求め方を習得することで、構造計算のスキルが飛躍的に向上します。
あなたの知識を確固たるものにするために、まずはこのページで学んでください。
【テストに出る】断面二次モーメントの「求め方」完全講義:積分と平行軸の定理、複合断面の計算手順を徹底解説

2. 学習効率を最大化する!構造力学の必携書籍
高専時代に力学を専攻し、現在も技術職としてキャリアを積んでいる私が、概念理解から計算までをスムーズに進めるために、実際に使って効果的だった書籍を厳選してご紹介します。
「独学で挫折しない」「図解が豊富でわかりやすい」という観点で選んでいます。




