支点反力の求め方をわかりやすく解説します【縦と横に分解しましょう】

支点反力の求め方は簡単です。

これだけ覚えておきましょう。明石高専の都市システム工学科（土木）で構造力学を学んだ僕がわかりやすく図解します。

支点反力の求め方をわかりやすく解説します

支点反力を求めるためには、その問題の力を全て絵で描くことが重要です。

支点反力を求める基本：全部の合計が０になること

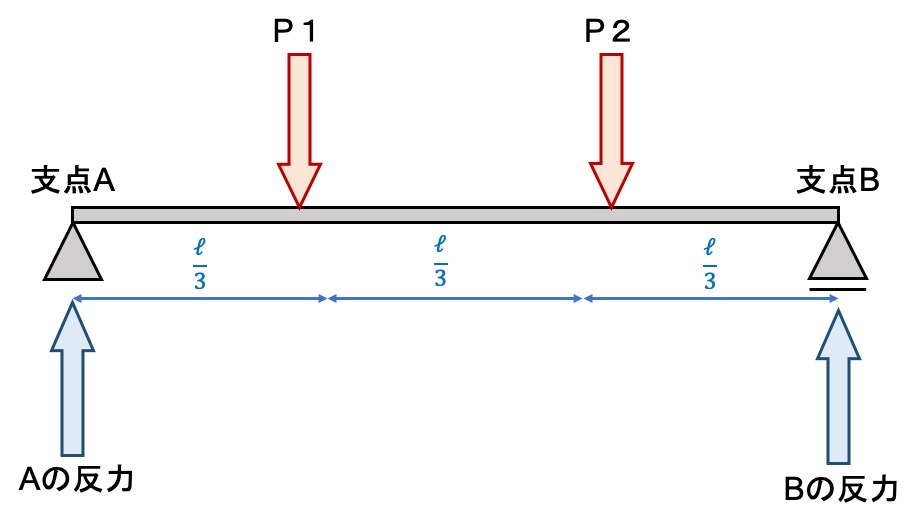
支点反力を求めるために必要なポイントは次の３つです。

力を全て絵（矢印）で書く

図にかかっている力を正しく書きましょう。上の図の場合、P1とP2がはりを上から押しているので、支点AとBは上向きに支えているはず。

なので、上向きに矢印を書きましょう。

力を縦と横に分解する

力を縦と横に分解しましょう。縦にはV（Vertical)、横にはH（Horizon）を使います。

上の図の場合は、斜めの力がないので、シンプルにできますが、斜めの力がかかっている場合は、\( \sin \)、\( \cos \)、\( \tan \)を使って分解します。

関数	３０°	４５°	６０°
sin（縦の力）	\( \dfrac{\sqrt{3}}{2} \)	\( \dfrac{\sqrt{2}}{2} \)	\( \dfrac{1}{2} \)
cos（横の力）	\( \dfrac{1}{2} \)	\( \dfrac{\sqrt{2}}{2} \)	\( \dfrac{\sqrt{3}}{2} \)
tan（あまり使わない）	\( \dfrac{\sqrt{3}}{3} \)	\(１\)	\( \sqrt{3} \)

例えば、４５°の斜め上方向に２kNの力が働いている時、縦と横の力は次のようになります。

縦と横と回転のそれぞれの力で方程式を作る

下の画像にあるように力が働いても、物が動かなければ力がつり合っていると言います。

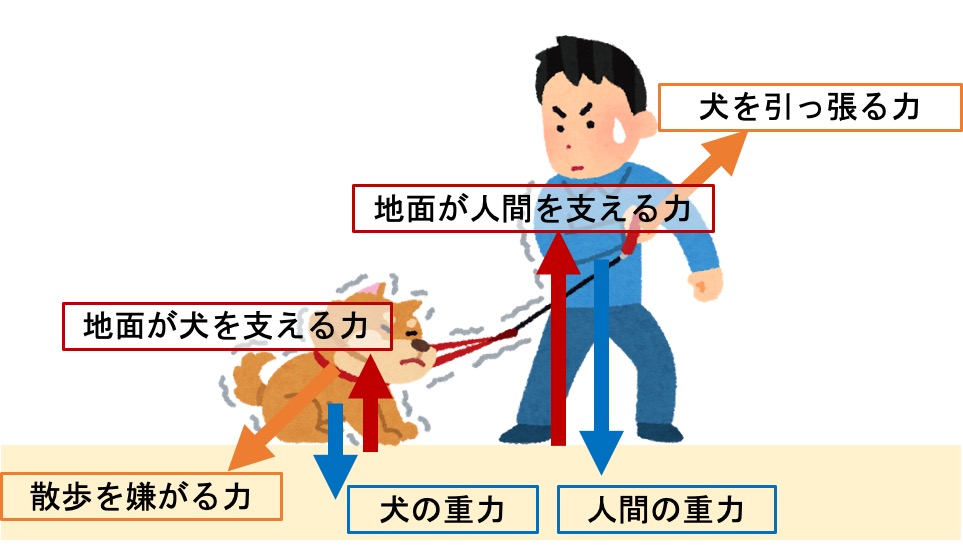
力のつり合いには次の３つがあります。

この３つの力がつり合っているから梁が動きません。回転は『力の大きさ×距離』で計算できます。

また、梁を支える『支点』には次の３種類があり、それぞれ次の力に抵抗します。

この力のつり合いを利用してはりの支点反力を求めます。

力のつりあいについては、『力のつり合いは絵で描くとわかる【構造力学の基礎】』が参考になります。

はりの支点反力の求め方：実例

はりにかかる力を具体的に次の数値にします。

１つのはりに５kNと８kNの２つの力が働いています。この時の支点反力Aと支点反力Bを求めてみましょう。

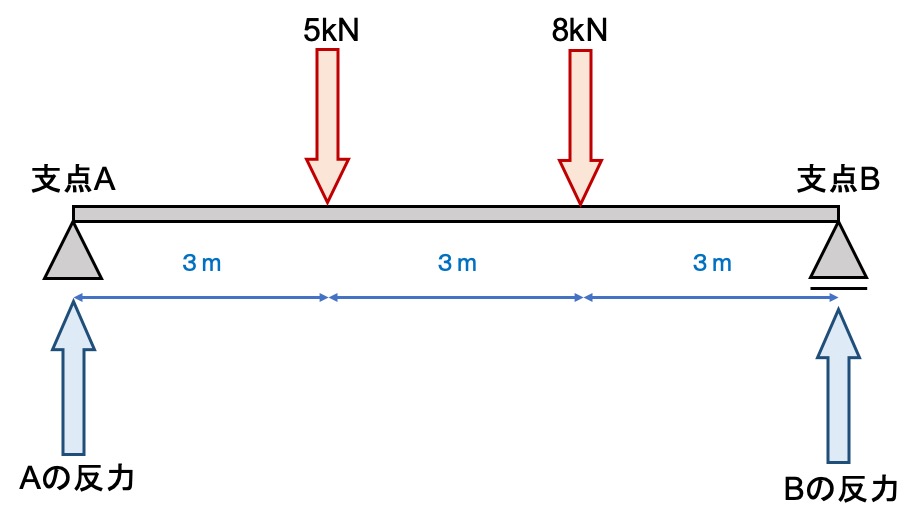
支点反力の求め方①力を全て書く

支点Aはヒンジ支点（縦と横に抵抗する）です。今回は横の力が働いてないので、横の力は０です。支点Aは縦の力が発生します。

支点Bはローラー支点です。縦の力だけに抵抗します。

まとめると以下の通り。

支点反力の求め方②力を縦と横に分解する

今回は斜め方向の力が働いていないので、スキップします。

支点反力の求め方③縦と横のそれぞれの合計が０になる

今回の場合は以下の通りになります。

縦の力は単純ですね。回転の力について深掘りします。

回転の力の計算方法

回転の力は『力の大きさ×距離』で計算できます。計算しやすい基準の場所を見つけて、そこからの回転の力を計算してみましょう。

今回は支点Aを基準にして回転の力を計算してみましょう。回る方向ごとに考えてみます。

まとめると、力のつり合いの式は以下の式です。

V_A+V_B=５_kN＋８_kN

V_A ×０_m+V_B×９_m=５_kN×３_m＋８_kN×６_m

これを解くとV_AとV_Bは次のようになります。

V_A＝6_kN

V_B＝７_kN

これで、はりの支点反力が求められました。

まとめ：支点反力の求め方は簡単

支点反力の求め方をまとめます。

これだけでOKです。

力のつりあいについては、『力のつり合いは絵で描くとわかる【構造力学の基礎】』が参考になります。

構造力学は問題を解けば理解できる

苦手だからと避けないで、簡単な問題をちょっとずつ解いてみましょう。

構造力学が苦手なら、この問題集が優しくて簡単です。

また、『構造力学が苦手な人が読むべきオススメ参考書5選』では、構造力学全般にオススメの参考書を紹介してます。