構造力学を学ぶ学生の皆さん、こんにちは。
断面二次モーメントの計算で手が止まっていませんか? 複雑な積分、ややこしい図心軸、そして何より「平行軸の定理」の使いこなし。構造力学の中でも、ここでつまずく学生は非常に多いです。
実は、私(明石高専卒)も、かつて断面二次モーメントが一番の苦手科目でした。しかし、期末テストや単位認定試験で確実に点を取るには、この計算を避けて通れません。
苦手意識を克服し、無事に単位を取得した私の経験に基づき、この記事では「テストで確実に点数を取る」ための戦略と手順の完全講義をします。
この記事を読むことで、あなたは以下の3つのスキルを習得できます。
- 基本公式を暗記し、瞬時に使えるようになる方法
- 最も間違いやすい平行軸の定理と図心軸からの距離を正しく求める方法
- T型断面やH形鋼などの複合断面を、ミスなく計算しきる手順
それでは、一緒に構造力学の勉強を始めましょう。あなたの苦手意識を、合格点に変えましょう!
目次
なぜ断面二次モーメントでつまずく?苦手克服のための心構え

構造力学で「苦手だ」と感じる人は、計算の複雑さよりも、「そもそも何をやっているのかわからない」という根本的な疑問からつまずいていることがほとんどです。
計算に進む前に、あなたの苦手意識を解消するための心構えと、断面二次モーメントの基本的な概念を解説します。
断面二次モーメントと断面一次モーメントの決定的な違い
多くの学生が最初に混乱するのが、断面一次モーメントと断面二次モーメントの混同です。筆者の経験からも、これを混同すると計算が破綻します。
結論から言うと、この2つは役割が全く違います。
| 項目 | 断面一次モーメント | 断面二次モーメント |
|---|---|---|
| 定義式 | \( S = \int y dA \) | \(I = \int y^{2} dA\) |
| 役割 | 図心(重心)の位置を求める | 剛性(曲げにくさ)を示す |
| 単位 | 距離の1乗 | 距離の2乗 |
断面一次モーメントは「図心を見つけるための道具」、断面二次モーメントは「剛性(曲げにくさ)を評価するための道具」と、目的で分けて覚えましょう。
【テスト攻略法】断面二次モーメントの基本公式と導出の方法

私が構造力学のテストで安定して点を取れるようになったのは、「暗記すべきところと、理解だけで良いところ」を明確に分けたからです。
ここでは、テストを突破するためにあなたがまず取るべき行動(暗記)と、その裏付け(導出)について解説します。
テストで点数をとるための鉄則:基本図形(長方形・三角形)の公式は暗記
テストで確実に点数を取るための筆者の戦略は、「基本図形の公式は暗記する」ことです。
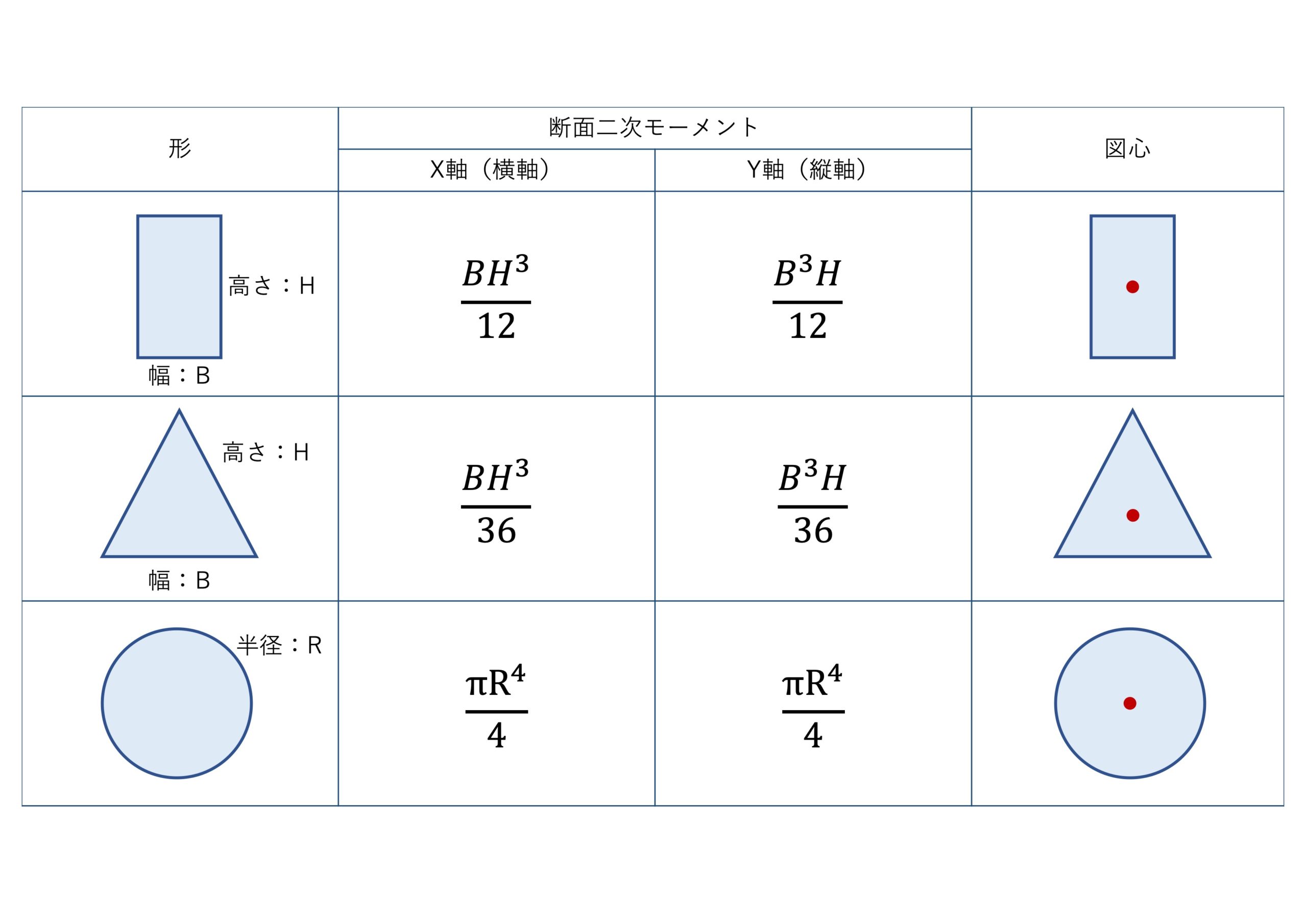
この公式は暗記必須です。特に長方形の公式 \(I_{G} = \frac{bh^3}{12}\) は、平行軸の定理で最も使うため、完璧に頭に入れておきましょう。
テスト対策を効率化したい方へ
構造力学の基礎公式がコンパクトにまとまっている参考書があると、暗記効率が格段に上がります。公式の確認や簡単な問題演習に最適です。
積分による導出:「なぜその公式になるのか」を知りたい人へ
公式を暗記するにしても、一度は導出の理屈を知っておくべきです。
ここでは長方形を例に、断面二次モーメントの定義式 \(I = \int y^{2} dA\) を使った導出プロセスを解説します。

その他の図形の断面二次モーメントの導出はこちらで解説しています。
複雑な形の断面二次モーメントは「平行軸の定理」で解こう
断面二次モーメントの計算で最も重要かつ最も間違えやすいのが、この平行軸の定理です。
T型断面やH形鋼など、複数の図形が組み合わさった複合断面を解くためには、この定理を完璧に使いこなすことが必須となります。
ここで、定理の仕組みと、ミスを減らすための注意点を完全にマスターしましょう。
平行軸の定理の公式と図心軸からの距離の求め方
公式: \(I_{x'} = I_{G} + A y^{2} \)
- \(I_{G}\):その図形自身の図心軸に関する断面二次モーメント
- \(A\):図形の面積
- \(y \):図形自身の図心軸と、求めたい軸 $x'$ との距離
この定理は、図心を通る軸に関する二次モーメントを、それに平行な別の軸に関する二次モーメントに変換するためのものです。必ず、暗記した \(I_{G}\) からスタートします。
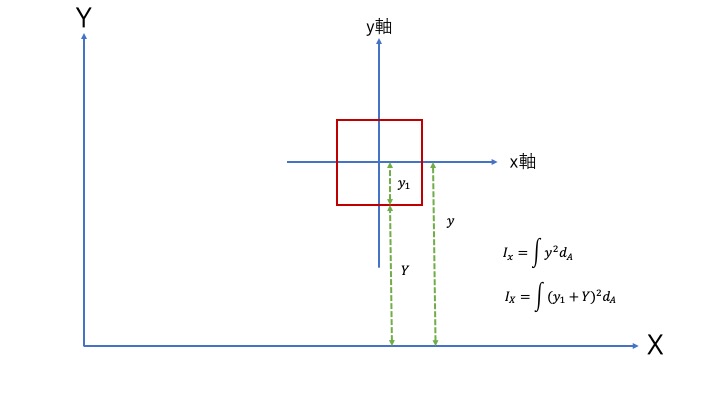
最も間違えやすい「図心からの軸のズレ」の注意点
平行軸の定理における最大のミスポイントは、距離 \(y\) の設定です。
\(y\) は「全体の図心軸」と「分割した部分図形の図心軸」の間の距離であり、決して基準軸からの距離ではありません。
計算を始める前に、断面全体の図心位置を正確に求めることが大切です。
【最重要】合成断面の計算手順と計算間違えをする3つの落とし穴

ここまで理解できれば、テストの高得点領域は目の前です。
ここでは、複雑な合成断面を解くための確実な手順と、私自身が何度も経験した「絶対に避けるべき3つの落とし穴」について具体的に解説します。
これらを実践すれば、あなたの構造力学の点数は飛躍的に向上します。
落とし穴1:基準軸の取り方(どこを \(y=0\) にするかで計算が変わる)
私は、合成断面の問題を解く際、断面の最も下端を必ず基準軸\(y=0\)として計算を始めていました。
基準軸を統一することで、全体の図心を求める際の計算ミスを防げます。全体の図心さえ正確に求まれば、平行軸の定理の\(y\)の計算が非常に楽になります。
T型断面の断面二次モーメントの計算例
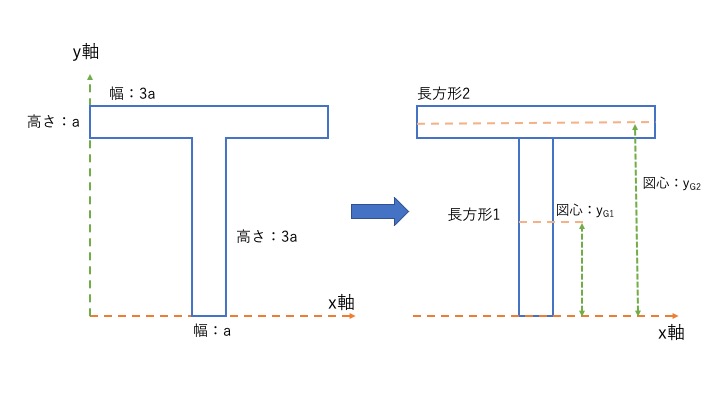
基準軸に対してそれぞれの長方形で断面一次モーメントを計算します。
全体の図心軸の計算は【断面一次モーメントの計算方法】意味・図心の求め方をわかりやすく解説しますで詳しく解説していますので、ぜひ参考にしてください。
長方形1の断面1次モーメントは、\(G_{x1} =A_{1} \times y_{1}\)より、\(G_{x1} = 4.5a^{3}\)
長方形2の断面一次モーメントは、\(G_{x2} =A_{2} \times y_{2}\)より、\(G_{x2} = 10.5a^{3}\)
なので全体の図心は、\(4.5a^{3} + 10.5a^{3}) = (3a^{2} + 3a^{2}) \times y_{G}\)で求められるので、\(y{G} = 2.5a\)
基準軸から\(2.5a\)の位置に図心軸があることが求められます。
各部分の基準軸との距離を求める
各部分と図心軸の距離は以下のようになります。
- 長方形1:\(1a\)
- 長方形2:\(1a\)
平行軸の定理を使って合成する
\(I_{i} = I_{Gi} + A_i \times a_{i}^{2}より
\( I_{T字} = \frac{a^{4}}{12} + 3a^{2} \times a^{2} + \frac{a^{4}}{12} + 3a^{2} \times a^{2}\)
なので、\( I_{T字} = \frac{2a^{4}}{3} \)となります。
落とし穴2:単位換算のミス( \(m \to mm\) での\(10^{12}\) の付け忘れ)
土木系や機械系の問題では、寸法を$m$(メートル)で与え、答えを\(mm^{4}\)(ミリメートル4乗)で要求することがよくあります。
- \(1 m^{4} = 10^{12} mm^{4}\)
計算途中で単位が混ざると、最後に \(10^{12}\) を掛け忘れるなどの致命的なミスに繋がります。私は、計算を始める前に全ての値を\(mm\)に統一していました。単位の確認は何度も行うようにしましょう。
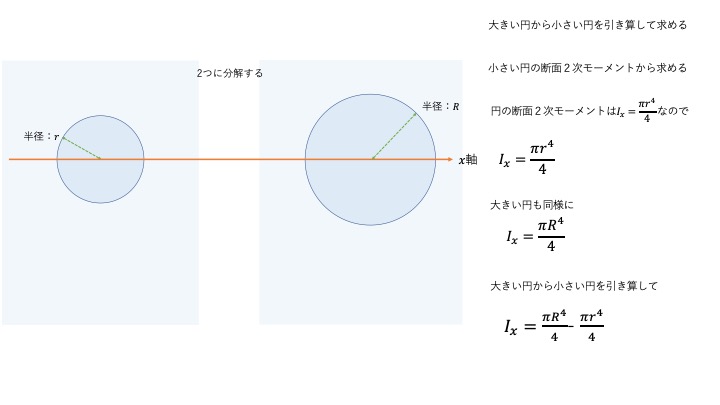
落とし穴3:穴抜き断面の処理方法(足し算か引き算か)
穴抜き断面(ボックス断面など)は、分割した図形を「足し合わせる(合成)」のではなく、「大きな図形から小さな図形を \(I_{x'} = I_{G} + A y^{2}\) の計算後に差し引く(引き算)」のが鉄則です。
応用問題をさらに解きたい方へ
テストで差がつくのは、やはり応用問題です。合成断面や穴抜き断面の計算例題が豊富な問題集で反復練習を積むことで、本番でのミスが激減します。
断面二次モーメントについてよくある質問(FAQ)

複雑な計算を終えたところで、最後に学生の皆さんが抱きやすい基礎的な疑問や、関連知識に関する質問にまとめて回答します。
Q1. 断面二次モーメントの「意味」と「単位」は何ですか?
(回答):
- 意味:断面形状による部材の曲げにくさ(剛性)を表す値です。
- 単位:\(mm^{4}\)や\(m^{4}\)といった「距離の4乗」で表されます。
Q2. 断面二次モーメントと断面係数の違いを教えてください。
(回答):
\(I\)(断面二次モーメント)は剛性(変形しにくさ)を評価しますが、\(Z\)(断面係数)は強度(破壊しにくさ)を評価する指標です。曲げ応力を計算する際に\(Z\)を使用します。
断面係数については、【元高専生が解説】断面係数とは?「応力」計算で必須の公式、断面二次モーメントとの違いを徹底図解で詳しく解説しています。
Q3. 断面二次モーメントが「大きいほど」構造的にどうなりますか?
(回答):
断面二次モーメント \(I\) が大きいほど、その梁や柱はたわみにくく(変形しにくく)なります。H形鋼が、効率よく\(I\)を稼げる断面としてよく用いられます。
まとめ:断面二次モーメントの求め方と次のステップ

断面二次モーメントは、構造力学の基礎であり、避けて通れない関門です。
私自身が経験したように、苦手意識を持つ必要はありません。この記事で解説した「暗記」「統一」「ミスの回避」の戦略を活用すれば、必ず点数が取れます。
- 暗記した公式をもう一度見直す。
- 合成断面の計算例題を、ミスなく解けるまで反復練習する。
あなたの勉強を応援します!
独学で進めるのが難しいと感じたら、良質な参考書を使うのが最も効率的です。筆者が学生時代に「これがあればよかった!」と感じた構造力学の最強参考書を厳選して紹介しています。
この記事が、あなたの構造力学の単位取得に貢献できることを願っています。頑張ってください!



