【元高専生が解説】断面係数とは？「応力」計算で必須の公式、断面二次モーメントとの違いを徹底図解 written by Totan BETTERKISO

断面係数は、部材の「強度」を計算するために必須の基礎概念ですが、公式（ \(\sigma = \frac{M}{Z} \) ）はシンプルなのに、「なぜこの概念が必要なのか？」「断面二次モーメントとどう使い分けるのか？」が掴みにくいと感じていませんか？

私自身、明石高専の都市システム工学科で構造力学の授業を受けているときに、この断面係数と断面二次モーメントの混同で何度も計算ミスをした経験があります。

この記事では、私がつまずいたポイントを徹底的に図解し、断面係数の定義から応力計算における役割、そして混同しやすいポイントまでを、わかりやすく解説します。

この記事を読めば、計算ミスを減らし、構造力学の基礎を確実に固められます。

まずは、断面係数の「定義」と「役割」という基本から見ていきましょう

断面係数とは？定義と応力計算における役割
断面係数の基本公式と長方形断面の求め方
- 長方形断面の公式 \(Z = \frac{b h^2}{6}\) の導出の考え方
- 長方形の具体的な計算例と手順
【最重要】断面二次モーメントとの決定的な「違い」
- 定義の違い：強度（Z）と剛性（I）
- 高専生時代の経験談：私がこれで混同を解消した「使い分けのコツ」
代表的な断面形状の断面係数と実践的な知識
断面係数をマスターするためのFAQ
まとめ：断面係数とは？「応力」計算で必須の公式
- 次のステップ：もっと構造力学を深く学ぶために

断面係数とは？定義と応力計算における役割

断面係数は、構造力学を学ぶ上で最初に覚えるべき重要な値です。このセクションでは、「断面係数とは何か？」という定義から、「なぜこの値が重要なのか？」という応力計算における役割までを分かりやすく解説します。

断面係数（Section Modulus：Z）とは、梁などの部材が曲げられたとき、どれくらいの力に耐えられるかを示す指標です。

簡単に言えば、「部材の曲げに対する強さ」を表す値です。

部材に大きな曲げモーメント（M）がかかっても、断面係数（Z）が大きいほど、部材は壊れにくく、より強い設計であると言えます。

なぜ必須なのか？：最大曲げ応力との関係

断面係数が構造計算で必須とされる最大の理由は、部材にかかる最大の応力（\(\sigma\)）を求めるためです。

構造力学において、部材にかかる応力（内部の力）が材料の許容応力を超えると破壊が発生します。この応力は、以下のシンプルな公式で計算できます。

\(\sigma = \frac{M}{Z}\)

\(\sigma\)：最大曲げ応力（部材が内部で抵抗している力）
\(M\)：最大曲げモーメント（部材に外からかかる曲げの力）
\(Z\)：断面係数（部材の形状によって決まる値）

この公式こそ、断面係数を学ぶ上で最も重要な式です。断面係数 \(Z\) が大きいほど、発生する応力 \(\sigma\) は小さくなることがわかります。つまり、\(Z\)が大きいほど、部材は頑丈ということです。

断面係数はどこで効いている？（応力の分布）

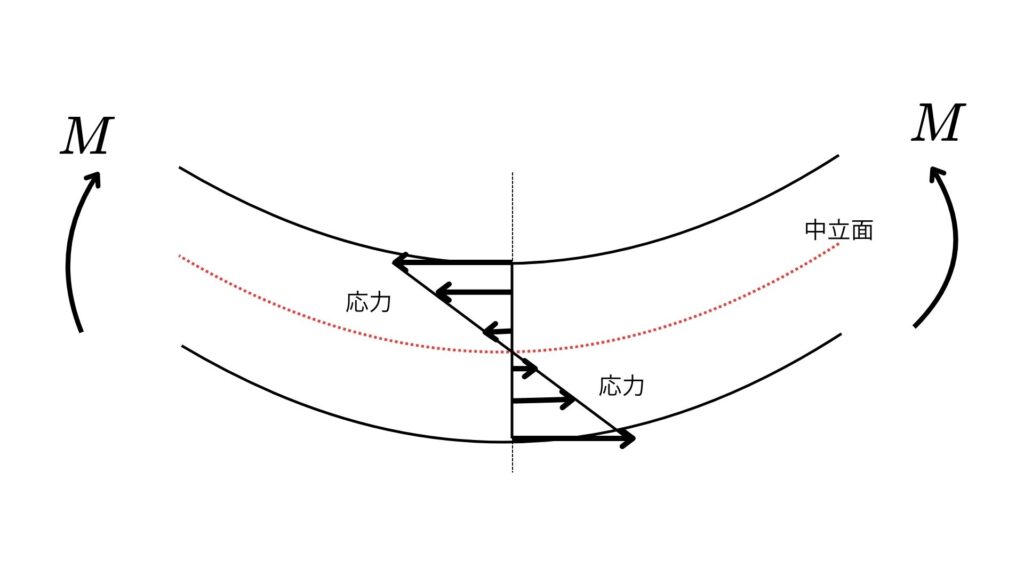
上記の図が示すように、曲げを受けた部材の断面では、応力は中心線（中立軸）でゼロになり、中立軸から最も遠い位置（最外縁）で最大となります。断面係数 \(Z\) は、この最大応力を算出するために特化した値なのです。

断面係数の「単位」と物理的な意味

断面係数の単位は\(cm^{3}\) や\(m^{3}\)など、長さの3乗になります。

この単位は、「断面二次モーメントの単位（\(cm^{4}\) ）」を「距離の単位（\(cm^{1}\) ）」で割った結果であると理解しておきましょう。

断面係数の基本公式と長方形断面の求め方

断面係数の計算は、最も単純な「長方形断面」の公式を理解することが出発点です。ここでは、公式がどのように導出されるかという考え方と、学生が陥りやすい計算ミスを防ぐためのコツを、私の経験を交えてご紹介します。

長方形断面の公式 \(Z = \frac{b h^2}{6}\) の導出の考え方

断面係数の公式は、断面二次モーメント（\(I\)）の公式を、中立軸から最外縁までの距離（\(y\)）で割ることで導出されます。

長方形断面の断面係数\(Z = \frac{b h^{2}}{6}\)

この導出プロセスを理解することが、公式の丸暗記から脱却する鍵です。

長方形断面の断面二次モーメント \(I = \frac{b h^{3}}{12}\)
中立軸から最外縁までの距離 \(y = \frac{h}{2}\)

長方形の断面二次モーメントの求め方は【テストに出る】断面二次モーメントの「求め方」完全講義で解説しています。

したがって、 \(Z = \frac{I}{y}\) に代入すると、 \(Z = \frac{b h^{2}}{6}\) が導かれます。

長方形の具体的な計算例と手順

実際に計算してみましょう。

幅 \(b = 10 cm\)
高さ \(h = 30 cm\)

の場合、断面係数\(Z\) は？

公式に代入する

\(Z = \frac{b h^{2}}{6}\)

\(Z = \frac{10 cm \times 30 cm)^{2}}{6}\)

計算を行う

\(Z = \frac{10 \times 900}{6} = \frac{9000}{6} = 1500 cm^{3}\)

【解答】\(Z = 1500 cm^{3}\)

この計算例は、断面係数を求める基本となります。特に、高さ \(h\) が2乗（\(h^{2}\)）される点に注目してください。

💡 元高専生コラム：計算ミスを減らす3つのチェックポイント（私の失敗談から）

構造力学の試験では、公式を知っていても計算ミスで点数を落とす学生が多いです。私も高専時代、これで苦労しました。

指数（べき乗）の確認：\(I\) は \(h^{3}\)（3乗）、\(Z\) は \(h^{2}\)（2乗）です。公式を書き出すたびに、指数を意識しましょう。
分母の確認：\(I\) は 12、\(Z\) は6です。これも混同しやすいポイントなので、「ZはIを割るから分母が小さくなる」と関連付けて覚えましょう。
単位の確認（\(h^{2}\) の二乗忘れ）:特に高さ \(h\) の二乗忘れによる計算ミスが多いです。計算結果の単位が \(cm^{3}\) になることを常にチェックしてください。

【最重要】断面二次モーメントとの決定的な「違い」

構造力学の学生が最もつまずき、混同しやすいのが、「断面二次モーメント」と「断面係数」の違いです。この二つの概念の定義と役割を明確に区別し、試験やレポートで迷わないための「使い分けのコツ」を伝授します。

定義の違い：強度（Z）と剛性（I）

断面係数\(Z\) と断面二次モーメント\(I\) は、どちらも断面の形から決まる値ですが、用途（役割）が決定的に違います。

項目	断面二次モーメント（I）	断面係数（Z）
役割	剛性（たわみにくさ）を示す	強度（壊れにくさ）を示す
計算で使われる式	たわみ（\(\delta\)）を求める式	応力（\(\sigma\)）を求める式
部材の設計	変形を抑える（梁が垂れ下がらないようにする）	破壊を防ぐ（部材が折れないようにする）
単位	\(cm^{4}\)（長さの4乗）	\(cm^{3}\)（長さの3乗）