構造力学を学習されている方の多くが、断面一次モーメントの公式 \(G=A \times y_{G}\) は知っているけれど、なぜそうなるのか(公式の根拠)を知りたい」と感じているのではないでしょうか。
この記事は、その疑問を解消するためにあります。
物理学や構造力学の基礎を深く理解するには、微積分を用いた「定義式」に立ち返ることが不可欠です。本記事では、断面一次モーメントの定義である積分 \( G =\int ydA \)を中心に解説します。
抽象的な「力のモーメント」の考え方から、最終的に長方形や三角形の公式がどのように導出されるのかを、ステップを追って丁寧に解説します。
目次
断面一次モーメントの「定義式」とは?
断面一次モーメントの公式 \(G=A \times y_{G}\)は非常に便利ですが、まず「断面一次モーメントとは何なのか?」という本質を理解しましょう。この定義の根幹にあるのが、微積分を使った「力のモーメント(回転力)」の考え方です。
積分という難しい言葉に抵抗があるかもしれませんが、ここでは「面積の持つ回転力の計算」という視点で、その役割を理解してください。
断面一次モーメントは面積の回転力を足し合わせている
断面一次モーメントの定義は、難しそうな積分記号を使いますが、やっていることはシンプルです。
構造物で「モーメント」といえば、回転させようとする力のことです。断面一次モーメントは、断面の各部分が基準軸の周りでどれだけ回転したがっているか(力のモーメント)を計算しています。
断面一次モーメントの定義は、微小な面積 \(dA\) と、その微小面積の基準軸からの距離 \(y\) を掛け合わせたものを、断面全体で無限に足し合わせる(積分する)というものです。
公式 \(G=A \times y_{G}\) は定義式から生まれた「ショートカット」
私たちが計算で使う便利な公式 \(G=A \times y_{G}\) は、上記の定義式から導き出されたものです。
図心の定義
物理学でいう重心(図心 \(y_{G}\))は、全ての重さ(面積)が、その一点に集まっていると見なせる点です。
定義式 \(G = \int ydA は、複雑な断面の回転力の総和を細かく求めているのに対し、公式 \(G=A \times y_{G}\) は、「全断面積 \(A\)」が「図心 \(y_{G}\)」という一点に集中していると見なして計算するショートカットなのです。
このように、定義式は複雑な「総和」の計算を、図心という概念を使ってシンプルにするための理論的な道具なのです。
基本的な図形の断面1次モーメント公式の導出・計算方法
断面一次モーメントの公式は以下の通り。
これだけだと、よくわからないですね。問題を解きながら詳しく解説します。
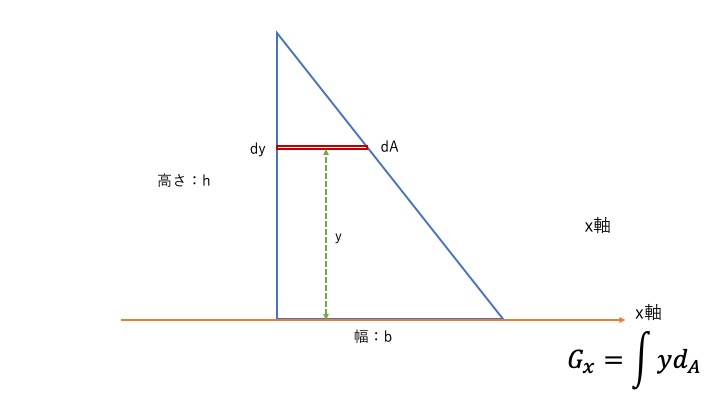
断面1次モーメントの導出と図心の計算①:四角形
簡単な四角形から計算してみましょう。こんな図形を考えます。

これを公式に当てはめると、
\(G_{x}=\int ydA\)
このままだと計算ができないので、\(dA\)をなんとかしましょう。
\(dA = 底辺b \times 高さdy\)と表現すると\(G_{x}=\int y \times b \times dy \)となります。
積分の範囲は\( 0 ~ h \)までなので、計算式は\(G_{x}=\int^{h}_{0}ybdy \)となります。
これで計算できますね。
\(G_{x}=\int^{h}_{0}ybdy \)
\(G_{x}=\left[ \dfrac{1}{2}by^{2}\right] _{0}^{h}\)
これを計算すると\(G_{x}=\dfrac{bh^{2}}{2}\)となります。
y軸に対する断面1次モーメントも同じように考える
\(G_{y}\)も同じように考えると、(G_{y}=\int xdA\)
\(dA = 高さh \times 底辺dx\)と表現すると\(G_{x}=\int y \times h \times dx \)となります。
これを計算すると\(G_{y}=\dfrac{b^{2}h}{2}\)となります。
四角形の図心は中心にくる
図心の公式は、\(\dfrac{G_{x}}{A}\)。ここで面積は\(bh\)なので、
こうなります。
断面1次モーメントの導出と図心の計算②三角形
では、三角形もやってみましょう。
\(dA\)が少し難しいですね。\(dA\)の高さは\(dy\)ですが幅が\(y\)の位置によって変化します。
なので、1次式で表現します。
\(dA\)=幅(\(-\dfrac{b}{h}y-b\))\(\times\)高さ\(dy\)と表現できます。
後は積分するだけ
ということで、三角形の断面1次モーメントを求める式は以下の通り
\(G_{x}=\int{h}{0}ydA\)
\(G_{x}=\int^{h}_{0}y(-(\dfrac{b}{h}y-b)dy\)
これを解くと、
\(G_{x}=\int^{h}_{0}yb-\dfrac{b}{h}y^{2}dy\)
\(G_{x}=\left[ \dfrac{1}{2}by^{2}-\dfrac{1}{3}\dfrac{b}{h}y^{3}\right] _{0}^{h}\)
\(G_{x}=\left[ \dfrac{1}{2}bh^{2}-\dfrac{1}{3}bh^{2}\right] \)
\(G_{x}=\dfrac{1}{6}bh^{3}\)
y軸に対する断面1次モーメントも同じ
図形を90度ひっくり返すと同じ計算ができます。つまり、\(b\)と\(h\)を入れ替えるだけ。
つまり、\(G_{y}-\dfrac{1}{6}b^{3}h\)です。
三角形の図心は\(\dfrac{1}{3}\)の位置にある
図心の公式は、\(\dfrac{G_{x}}{A}\)。ここで面積は\(\dfrac{1}{2}bh\)なので、
断面1次モーメントの導出と図心の計算③円
円は少しややこしいですが、一緒にやってみましょう。
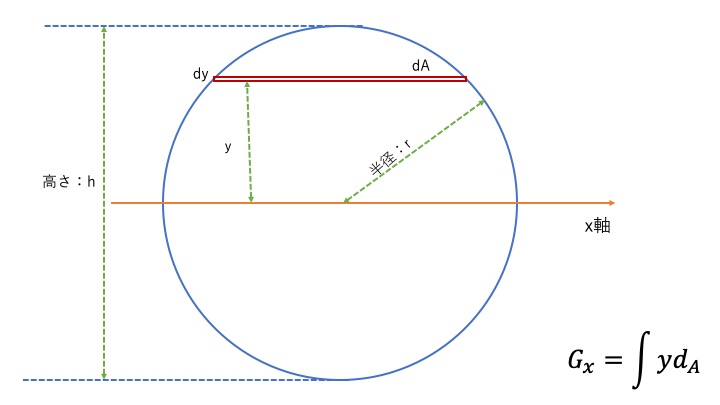
この時、三角関数を使って考えます。
\(x\)と\(y\)を三角関数(半径\(r\)と\(\theta\))に置き換えて考える
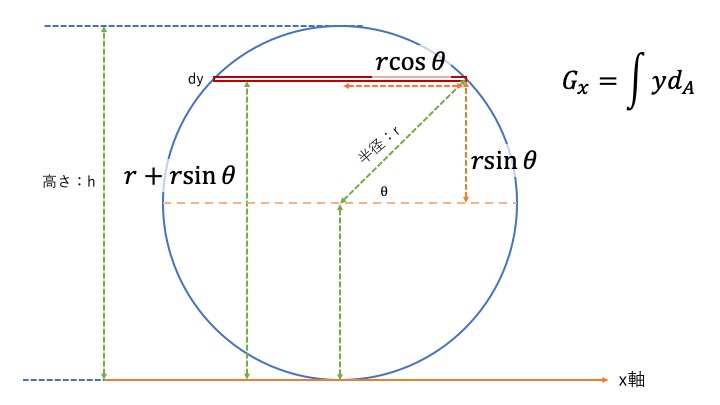
以下のようになります。
この場合、積分範囲は\(0~h\)だったものが、\(\dfrac{\pi}{2}~-\dfrac{\pi}{2}\)となります。
以上より、円の断面1次モーメントを求める式は、
\(G_{x}=\int^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}(r+r\sin(\theta)) \times 2r\cos(\theta)\times r\cos(\theta))\)
ややこしいですね。\(r\)をまとめて積分の外に出して、\(\sin\theta\)にまとめましょう。
\(G_{x}=2r^{3} \int^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}(1+\sin(\theta))(\cos^{2}(\theta))\)
\(\cos^{2}(\theta)=1-\sin^{2}(\theta)\)なので、
\(G_{x}=2r^{3} \int^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}(1+\sin(\theta))(1-\sin^{2}(\theta))\)です。
まとめると、
\(G_{x}=2r^{3} \int^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}(1-sin^{2}(\theta)+\sin(\theta)-sin^{3}(\theta) \)です。
2倍角、3倍角の公式を使って積分する
それぞれ積分しましょう。\(sin^{2}(\theta)\)とか\(sin^{3}(\theta)\)の積分は公式をカンニングします。
まとめると、
\(G_{x}=2r^{3} \left[ \theta - \dfrac{1}{2}\theta-dfrac{1}{4}\sin2\theta - -\cos\theta+\dfrac{1}{3}\cos^{3}\theta \right]_{\pi/2}^{-\pi/2} \)
ここで、\(\dfrac{\pi}{2}\)と\(-\dfrac{\pi}{2}\)のとき、\(\cos\theta=0\)、\(\sin2\theta=0\) なので、
\(G_{x}=2r^{3}\left[\dfrac{\pi}{2}-\dfrac{\pi}{4}\right]\)
\(G_{x}=\pi r^{3}\)
円の図心は中心にある
当たり前ですね。ですが、式で証明します。
図心の公式は、\(\dfrac{G_{x}}{A}\)。ここで面積は\(\pi r^{2}\)なので、
断面1次モーメントの導出と図心の計算④半円
半円もやっておきましょう。円と似た流れでできます。
これも三角関数を使います。
半円は三平方の定理を使う
円の時は三角関数を使いましたが、半円では三平方の定理を使いましょう。
この時、\(y\)の範囲は、\(0\)から\( r\)まで。
\(G_{x}=\int^{r}_{0} y \times 2\sqrt{r^{2}-y^{2}}dy\)
\(r^{2}-y^{2}\)を\(t\)として置換積分する
\(r^{2}-y^{2}\)置換積分すると\( \dfrac{dy}{dt}=-2y \)、つまり、\(dy = -\dfrac{1}{2y}dt\)となります。
範囲は\(y=0\)のとき\(t=r^{2}\)、\(y=r\)のとき\(t=0\)です。
\( G_{x} = \int^{0}_{r^{2}} 2y \times (-\dfrac{1}{2y}dt) \)
\( G_{x} = \int^{0}_{r^{2}} 2y \times \sqrt{t} \times (-\dfrac{1}{2y}dt) \)
\( G_{x} = \int^{0}_{r^{2}} - \sqrt{t} dt) \)
\( G_{x} = \int^{r^{2}}_{0} \sqrt{t} dt) \) (範囲を逆にして- を消しました。)
\( G_{x} = \left[ \dfrac{2}{3}t^{\dfrac{3}{2}} \right]^{r^{2}}_{0} \)
\( G_{x} = \dfrac{2}{3} r^{3} \)
半円の図心は\( \dfrac{4}{3\pi}r \) の位置にある
図心の公式は、\(\dfrac{G_{x}}{A}\)。ここで面積は\( \dfrac{1}{2} \pi r^{2} \)なので、
\( \dfrac{4}{3 \pi} = 0.4244....\)なので、真ん中よりも下に寄った位置に図心があるってことですね。
円、三角形、四角形の図心と断面1次モーメントのまとめ
代表的な断面1次モーメントと図心の位置です。とりあえず3つだけ覚えましょう。

まとめ:断面一次モーメントの公式導出は理解への一歩

本記事では、断面一次モーメントの定義式 \(G = \int ydA\)から、長方形・三角形といった基本図形の公式の導出方法について解説しました。
理論を理解する最大のメリットは、なぜ図心を通る軸に関する断面一次モーメントがゼロになるのかという、公式の持つ性質の根拠を、積分という数学的な必然性から説明できる点にあります。
理論の次は実践へ
公式の導出は学問的理解に不可欠ですが、実際の構造設計や定期テストにおいては、複雑なT字型やI型断面の実践的な計算が必須となります。その際は、分割した図形を\(G=A \times y_{G}\) で合成するという手法が最も有効です。
複雑な断面の具体的な計算手順や、その値が構造設計でどのように応用されるかについては、【断面一次モーメントの計算方法】意味・図心の求め方をわかりやすく解説しますをご覧ください。
積分による公式の導出は、構造力学の理論的な背景を深く理解するために不可欠です。


