
明石高専の都市システム工学科(土木)で構造力学を学んだ僕がわかりやすく図解します。
構造力学を学び始めた高専生・大学生、そして資格取得を目指す方が、まずつまずくのが支点反力(してんはんりょく)の計算ではないでしょうか?
構造力学の計算は、この支点反力から始まります。ここが分からないと、次に進む「せん断力」や「曲げモーメント」の計算も全てストップしてしまいます。土木技術者として、構造物の基礎設計に直結する最初の砦です。
この記事では、構造力学の基礎となる「支点反力」の求め方を、誰もが確実に解けるようになる3ステップで徹底的に解説します。初学者が陥りやすいモーメント計算のコツや、算前の鉄則を具体的にお伝えします。
この記事を読み終える頃には、あなたは単純梁だけでなく、片持ち梁や応用的な構造(ラーメン・トラス)の支点反力も自信を持って計算できるようになっているでしょう。
目次
支点反力とは?(定義と重要性)

「そもそも支点反力とは何か?」を理解することが、構造力学の学習をスムーズに進めるための土台となります。特に、構造力学の教科書に必ず出てくる3種類の支点(ローラー、ピン、固定)が、それぞれどのような反力を持っているのかを正確に把握しましょう。
支点反力とは何か?
土木建築物は、形に関わらず地上に静止して一定の位置を保つ必要があります。この状態を構造物が安定であると言います。構造物が安定であるのは、地盤と結合されているからで、この結合点を支点と言います。
一方で構造物は地盤に支えてもらっていますが、その反作用として地盤から力を受けています。この力を反力と言います。
つまり、支点が受ける反力を支点反力と言います。
3種類の支点について知ろう
この支点反力を知るために3種類の支点とその特徴を知りましょう。
| 支点の種類 | 上下左右方向 | 回転方向 | イメージ |
|---|---|---|---|
| ヒンジ支点(ピン支点) | 上下左右に動かない | 回転できる | 蝶番 |
| ローラー支点 | 転がる方向には動く | 回転できる | スケートボード |
| 固定支点 | 上下左右に動かない | 回転できない | 埋め込まれた棒 |
支点の種類によって反力の数が違う
それぞれの支点によって反力の数が異なります。
- ヒンジ支点:2つ(上下と左右)
- ローラー支点:1つ(転がらない向き)
- 固定支点:3つ(上下と左右と回転)
この違いも覚えておきましょう。
支点反力の求め方:構造力学の3つの基本

構造力学の基本は、物体は静止している(動いていない)という前提です。この「つり合い」の状態を数式で表現するのが、これから解説する3つのつり合いの公式です。計算でつまずかないための「力の矢印を全て書き込む」という鉄則を実践しながら、この3ステップを確実にマスターしましょう。
【STEP1】力のつり合い(鉛直・水平方向)を書き込む
まずは、物体に全ての力を書き込みましょう。
そうすれば、物体が静止している(右にも左にも、上にも下にも動かない)ので、それぞれの向きの力を合計すれば0になるはずです。
【STEP2】モーメントのつり合いを考える
物体が静止しているので、もちろん回転もしません。
なので、力のモーメント(力の大きさ✖︎距離)の合計も0になります。
力が密集しているところを基準にすると計算がラク
力の矢印が集中している点を基準にモーメントを考えましょう。
その点は距離が0になるのでモーメントを考えなくて大丈夫だからです。
【STEP3】反力(未知数)を求める連立方程式を解く
STEP1とSTEP2のつり合い式を連立方程式にして未知数を解きましょう。
この3ステップで解くことができます。
力のつりあいについては、『力のつり合いは絵で描くとわかる【構造力学の基礎】』が参考になります。
例題で解説:単純はりの支点反力の求め方
理論を学んだ後は、実際に手を動かして問題を解くことが最も重要です。
ここでは、構造力学の基本中の基本である単純はりの例題を解いてみましょう。
先ほど学んだ3ステップの公式を適用しながら、計算プロセスを具体的に追っていきます。シンプルな例題を完璧に解けるようになることが、応用問題への最短ルートです。
単純はりの支点反力を求めよう
はりにかかる力を具体的に次の数値にします。
1つのはりに5kNと8kNの2つの力が働いています。この時の支点反力Aと支点反力Bを求めてみましょう。
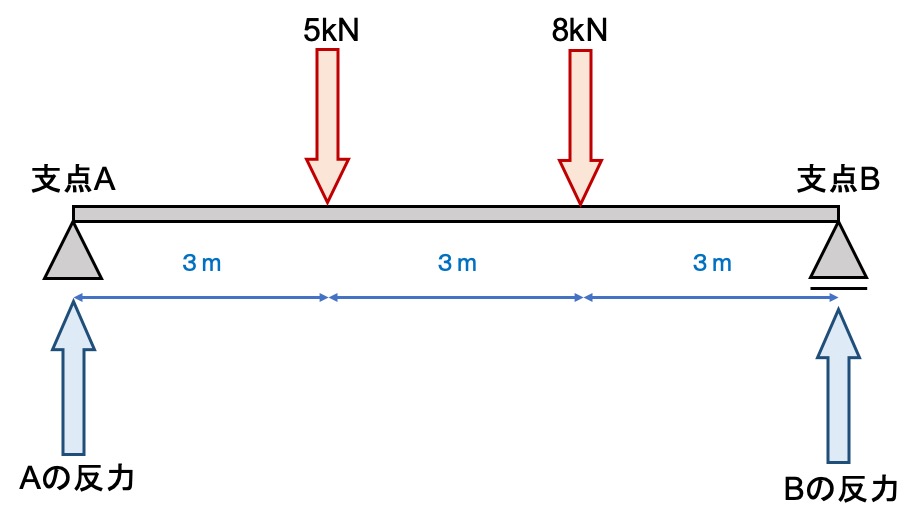
支点反力の特徴を考える
まずは、支点についてよくみてみましょう。
支点Aはヒンジ支点
支点Aはヒンジ支点(縦と横に抵抗する)です。今回は横の力が働いてないので、横の力は0です。支点Aは縦の力が発生します。
支点Bはローラー支点
支点Bはローラー支点です。縦の力だけに抵抗します。

支点の種類によって、抵抗する力の向きが変わります。気をつけましょう。
まとめると以下の通り。
支点反力の求め方②力のつり合い式を作る
矢印の向きに注目して、つり合い式を作りましょう。
上向きを左辺、下向きを右辺にまとめて足し算しましょう。
- VA+VB=5kN+8kN
支点反力の求め方③回転方向の力のつり合い式を作る
回転方向の力のつり合い式を作ります。
今回は支点Aを基準にして作ってみます。
左向きに回す力を左辺、右向きに回す力を右辺にして作ってみましょう。
- VA ×0m+VB×9m=5kN×3m+8kN×6m
回転の力の計算方法
回転の力は『力の大きさ×距離』で計算できます。計算しやすい基準の場所を見つけて、そこからの回転の力を計算してみましょう。
今回は支点Aを基準にして回転の力を計算してみましょう。
問題の図形の上にペンを置いて、支点Aを抑えながら力の矢印の方向に押して回る方向を考えてみましょう。

右回り=左回りとなるので、上の式になります。
支点反力の求め方④連立方程式を解く
まとめると、力のつり合いの式は以下の式です。
VA+VB=5kN+8kN
VA ×0m+VB×9m=5kN×3m+8kN×6m
これを解くとVAとVBは次のようになります。VA=6kN
VB=7kN
これで、はりの支点反力が求められました。
Q&A:支点反力のつまづきやすい疑問を解消

構造力学の学習でよくある疑問や、Q&A形式で解説します。計算サイトの利用法や、反力の「向き」の考え方など、計算中に迷いやすいポイントをここで解消し、知識を盤石なものにしましょう。
反力の「向き」はどっちを仮定すればいい?
向きに正解はありませんが、基本的に単純はりなら支点反力を上向きに取ると計算がしやすいです。
支点反力と断面力(せん断力・曲げモーメント)の関係は?
支点反力を求めると断面力を求めることができます。
断面力については『【断面力とは】断面力の求め方や応力との違いを解説』で詳しく解説しています。
まとめ:支点反力の求め方は簡単

本記事では、構造物の安全設計の基礎となる「支点反力」について、以下のポイントが重要であると解説しました。
- 力を全て書き込む
- 上下と左右の力のつり合いを考える
- 回転方向の力のつり合いを考える
構造力学の計算は、この支点反力さえ完璧にマスターすれば、次のステップである断面力(せん断力、曲げモーメント)の計算にスムーズに進むことができます。
力のつりあいについては、『力のつり合いは絵で描くとわかる【構造力学の基礎】』が参考になります。
重要:構造力学を体系的に学ぶには
「支点反力は理解できたけれど、構造力学全体を基礎から学び直したい」「他の公式やトラス、ラーメン構造の応用問題も解けるようになりたい」という方は、ぜひ【元高専生が教える】挫折しない構造力学の勉強法|テストで点数を取るロードマップをご覧ください。

また、『構造力学が苦手な人が読むべきオススメ参考書5選』では、構造力学全般にオススメの参考書を紹介してます。

