【図解】静定と不静定とは？見分け方から解き方のコツまで徹底解説

『静定』と『不静定』。構造力学を学び始めたばかりのあなたが、この2つの言葉を聞いて「一体何のこと？何が違うの？」と混乱してしまうのは当然です。先生の説明や教科書の内容が頭に入ってこず、テストでどう解けばいいのか分からず、困っていませんか？

実は、この2つは、構造力学のテストで確実に点数を取るための「カギ」となる最も重要な概念です。力のつり合いだけでは反力や応力が求められないのが不静定構造物で、逆に、力のつり合いだけで解が求まるものが静定構造物です。そして、その見分け方には簡単なコツがあります。

この記事では、元高専生である私が、静定と不静定の概念を初心者にもわかりやすく解説し、見分け方から解き方のコツまでを徹底的に解説します。この記事を読めば、あなたはもう静定・不静定の問題で悩むことはなくなるでしょう。

さあ、静定・不静定を完璧にマスターし、構造力学の次のステップへ進みましょう。

静定と不静定とは？初心者向けにわかりやすく解説

「静定」と「不静定」。これらの言葉は、構造力学を学び始めたばかりの学生にとって、混乱の元になりやすい言葉です。

簡単に言うと、構造物の反力や断面力は、「力のつり合いの式」を使って計算することができます。

このように、たった3つの力のつり合いの式で解けるかどうかが、静定と不静定を分ける大きな違いなのです。

静定構造とは？

静定構造物は、外部から力がかかっても、力のつり合いの式（ΣV=0、ΣH=0、ΣM=0）だけで、すべての反力や断面力を計算できる構造です。

身近な例: テーブルの脚が3本しかないと不安定ですよね。これは静定構造物と似ていて、力がかかったときにすべての反力が決まります。

静定構造は、計算が比較的シンプルで、構造物の挙動がわかりやすいという特徴があります。

不静定構造とは？

一方、不静定構造物は、力のつり合いの式だけでは、すべての反力を求めることができません。

この問題を解くには、「材料がどれくらい変形するか」という変位の条件を考慮する必要があります。そのため、計算は複雑になります。

身近な例: テーブルの脚が4本あると、どこか1本の脚が浮いてしまうことがありますよね。これは、4本目の脚が「余分な反力」として機能し、どれか1本の反力を外してもテーブルは安定を保つことができるからです。

不静定構造物は、一部の部材や反力が損傷しても倒壊するまでの余裕度が高いという特徴があります。そのため、力学的な安全性が高いとされています。

これらの見分け方のコツを組み合わせることで、あなたはどんな問題にも自信を持って立ち向かえるようになります。

【重要】静定と不静定の見分け方

構造力学のテストで静定・不静定の問題が出たとき、一瞬で正しく見分けることができれば、その後の問題をスムーズに解くことができます。

ここでは、私が実際に使っていた、誰でも簡単に静定・不静定を見分けるシンプルな考え方を解説します。難しい公式を覚える必要はありません。

判別式は不要！シンプルな「考え方」をマスターしよう

静定と不静定を見分けるカギは、「未知の力の数」と「解くための式の数」を比べることです。

構造力学の問題を解くために使える式は、たったの3つです。

この3つの式（方程式）を使って、未知の反力を求めます。

このように、複雑な公式を暗記するのではなく、反力の数と式の数を比べるというシンプルな考え方をマスターすれば、どんな問題にも対応できます。

【実践】未知の力を数えるための手順

ここでは、静定・不静定を判断するための具体的なステップを解説します。

それでは、実際に問題をみながら解いてみましょう。

【補足】判別式について

専門的な試験やより複雑な構造物では、以下の判別式を用いることで、より厳密に静定・不静定を判断できます。

m = r + 3n - 3j + s

mの数によって以下のように判別できます。

• m < 0 → 不安定構造
• m = 0 → 静定構造
• m > 0 → 不静定構造

静定・不静定問題の解き方と演習

静定と不静定の見分け方をマスターしたところで、いよいよ実践です。静定問題と不静定問題では、その後の解き方が全く異なります。

このセクションでは、静定と不静定、それぞれの問題の解法プロセスを具体的に解説します。

静定問題の解き方

静定問題は、3つの力のつり合い式だけで解くことができます。

1. 未知の反力をすべて書き出す: まずは、ピン支点やローラー支点、固定端などから生じる反力を、矢印で図に書き出しましょう。
2. 力のつり合い式を立てる:
   • ΣV = 0 (鉛直方向の力のつり合い)
   • ΣH = 0 (水平方向の力のつり合い)
   • ΣM = 0 (任意の点でのモーメントのつり合い)
3. 方程式を解く: 3つの式から未知の反力を求めることができます。

詳しくは、『【断面力とは】断面力の求め方や応力との違いを解説』で解説しています。

不静定問題の解き方

不静定問題は、力のつり合い式だけでは解けません。この問題を解くには、材料の変形を考慮した式を使う必要があります。

この問題を解く方法はいくつかありますが、ここでは代表的なアプローチを2つ紹介します。これらの解法については、それぞれ別記事で詳しく解説します。

適合条件式を使う方法

余分な反力や部材を一度取り除き、その場所に「適合条件」と呼ばれる、元の状態に戻すための変位を考え、連立方程式を解く方法です。

重ね合わせの原理を使う方法

元の不静定問題を、いくつかの静定問題に分解して、それぞれの問題を解いてから答えを重ね合わせる方法です。

不静定実際に問題を解いてみよう【練習問題】

以下の問題を解いてみましょう。

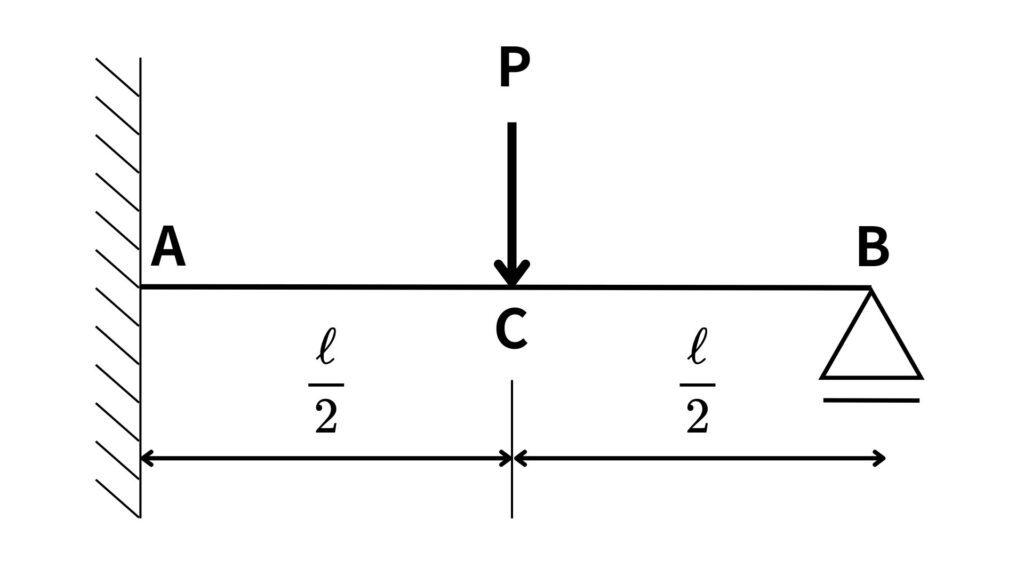
ここでは、適合条件を使った解き方で進めます。図で解説するので一緒に解いてみましょう。

基本的な方針は以下の通り。

たわみの求め方については『【構造力学】微分方程式でたわみを解く』で解説しています。

1つずつ解説します。

自由物体図を書いて釣り合い式を作る

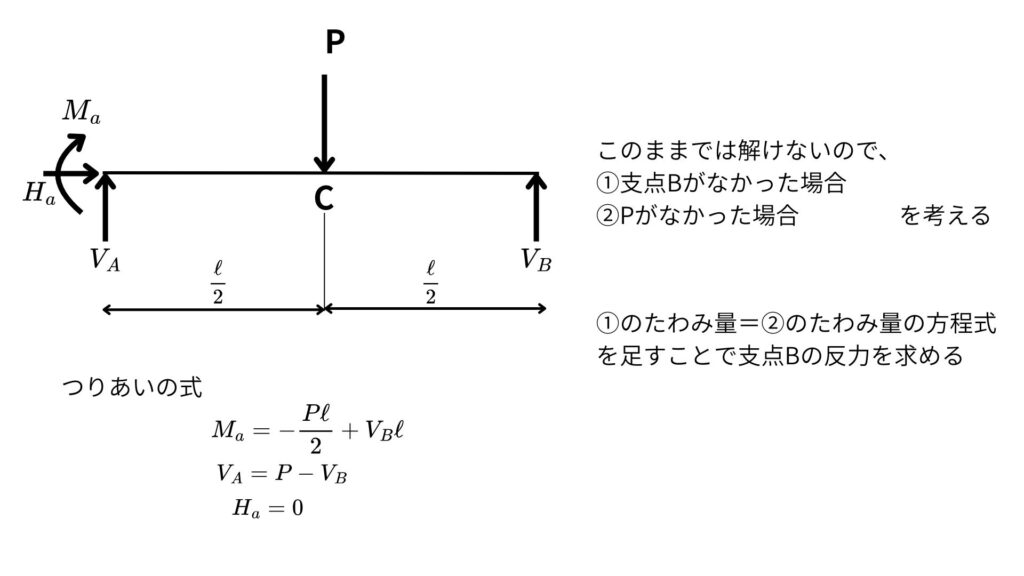
支点Bがなかった場合を考えて点Bのたわみ量①を計算する

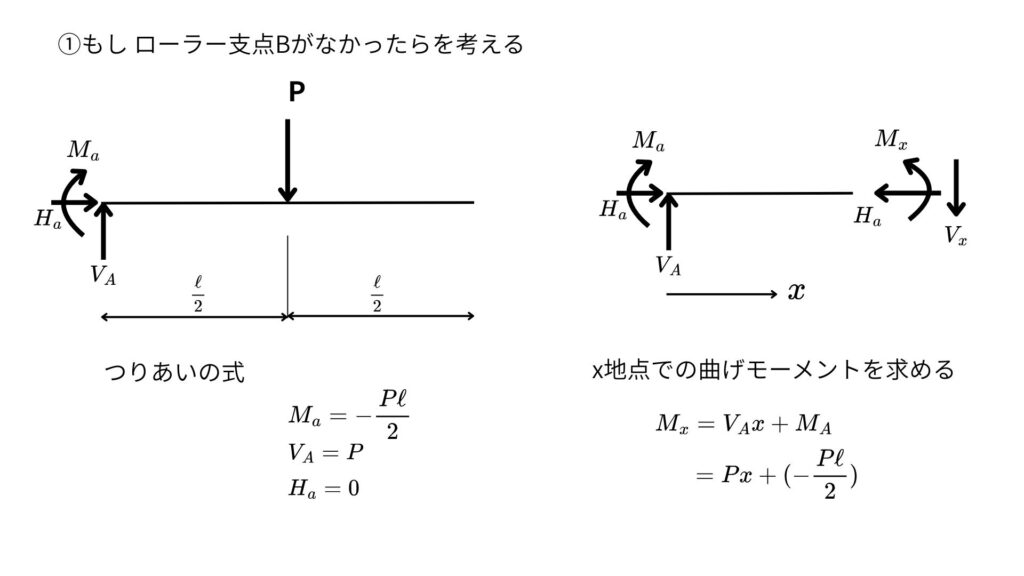
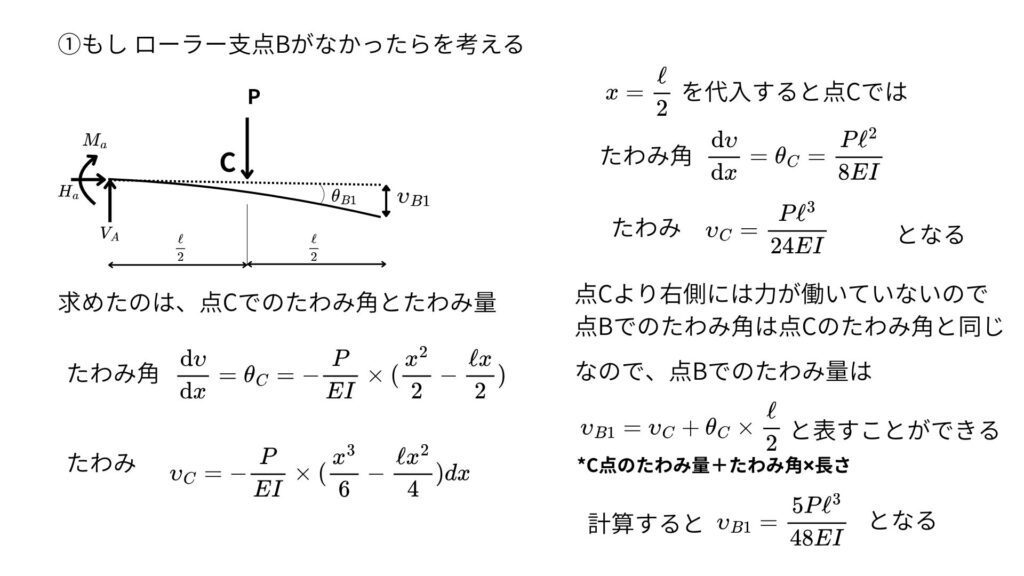
Pがなかった場合を考えて点Bのたわみ量②を計算する

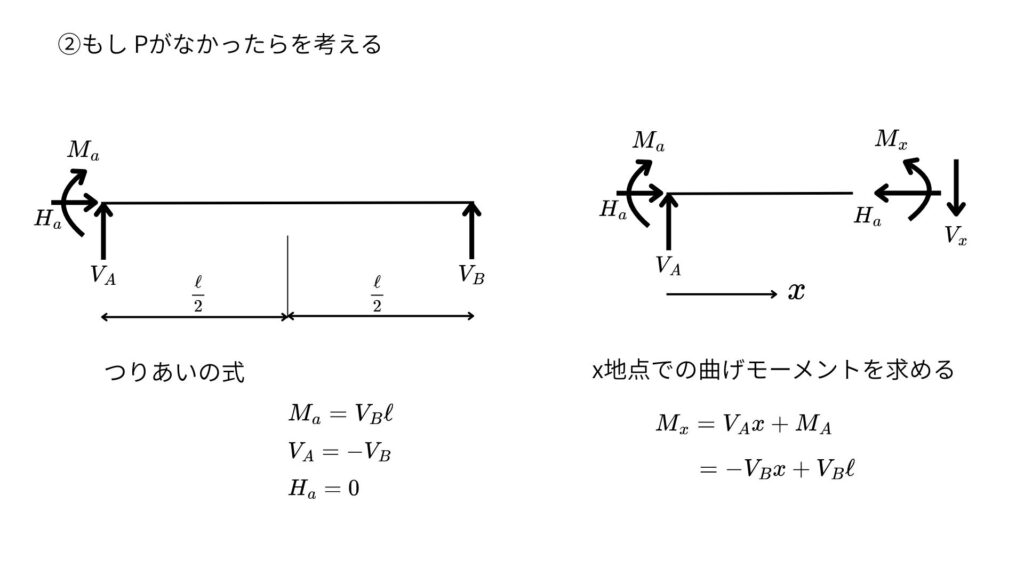
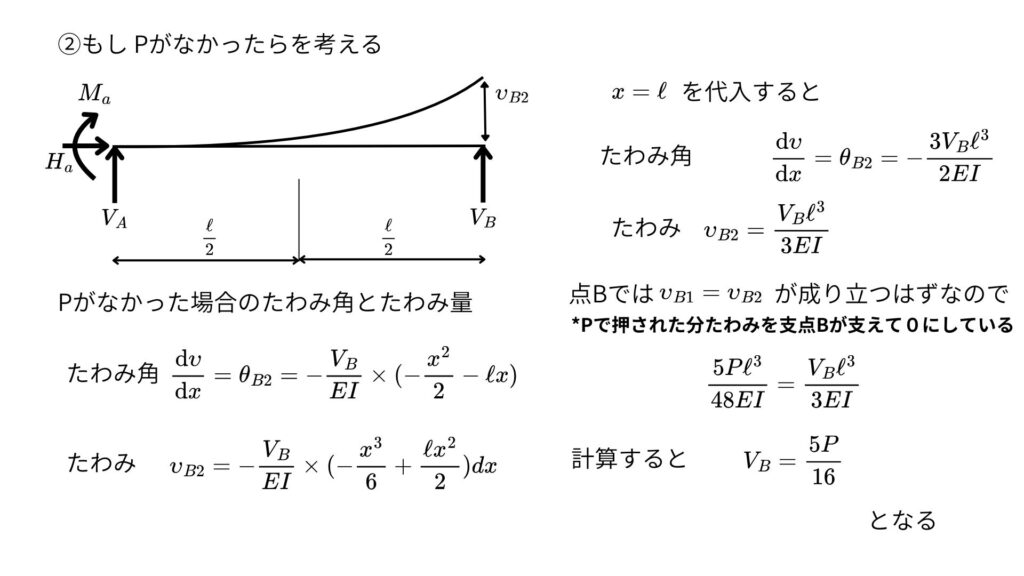
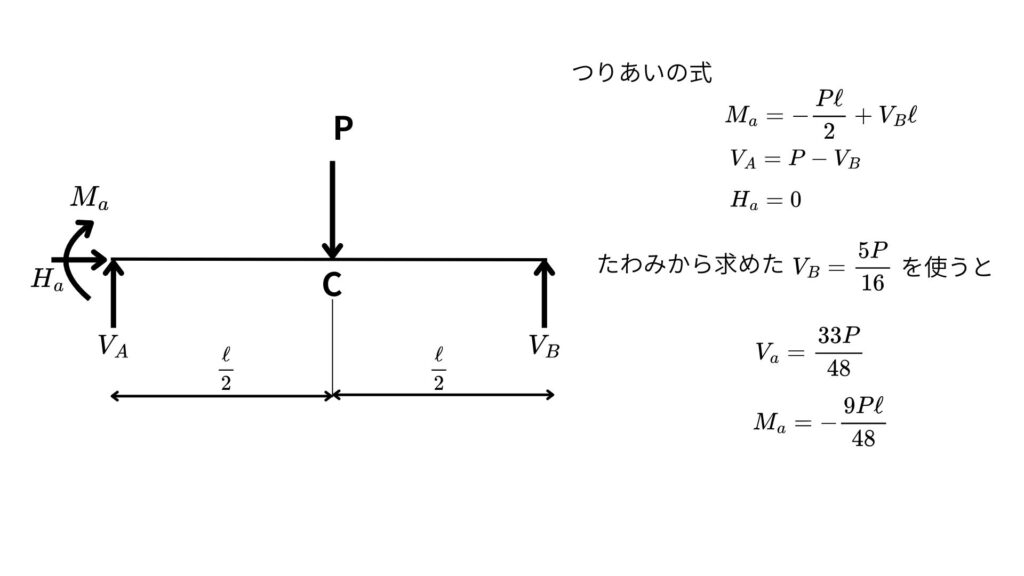
釣り合い式から支点Aの反力を求める

静定と不静定を理解するコツ

ここまで、静定と不静定の概念から見分け方、そして解法までを解説してきました。

構造力学を学び始めたばかりの頃、私はこれらの概念を理解するのにとても苦労しました。しかし、あることに気づいてからは、一気に構造力学が楽しくなりました。

それは、構造力学は、複雑に見えても、実はシンプルな原理の応用でしかないということです。

複雑な問題も「シンプルに考える」ことが重要

テストで一見難しそうな問題に出会ったとき、頭が真っ白になってしまうことがありますよね。そんなときこそ、一度深呼吸をして、立ち止まってください。

そして、この記事で学んだ「未知の力の数」と「解くための式の数」を比べるというシンプルな考え方に戻ることを意識してください。そうすれば、複雑に見えた問題も、必ず解法の糸口が見えてきます。

あなたの直感を信じよう

構造力学は、「なぜそうなるか」を理解することが何よりも重要です。

• なぜこの支点だと反力が3つになるのか？
• なぜこの構造物は不安定なのか？

教科書や公式を覚えるだけでなく、単純に考えるとどうなる？ということを頭の中でイメージする習慣をつけましょう。あなたの直感は、問題を解く上で最も強力な武器となります。

最後に｜構造力学の学習を次のステップへ

静定・不静定の概念を理解できたあなたは、もう構造力学でつまづくことはありません。

さて、次に何から始めればいいか迷っているあなたへ。私が高専時代に本当に役立った教材と、構造力学の全体像を掴むためのロードマップをまとめました。

【元高専生が厳選】学習に役立つ書籍

構造力学の独学にオススメの書籍を紹介します。

この本は、構造力学の基礎を固める上で、読みやすい一冊です。豊富な図と丁寧な解説で、独学でも挫折しないように工夫されています。静定・不静定の「考え方」をより深く学び、基礎から応用まで着実に力をつけたいあなたに、心からおすすめします。

構造力学を学習する上で、自分の手を動かして解く作業は欠かせません。この本は、構造力学が苦手なあなたにも分かりやすく取り組みやすい書き込み式問題集です。

【あわせて読みたい】構造力学の全体像を掴むロードマップ

こちらの記事では構造力学を基礎からまるっと解説しています

この記事の内容で分からない点や、次に進むべき方向性について相談したいことがあれば、ぜひコメント欄で教えてください。