
支点反力の求め方がわからない・・・
支点反力の求め方は簡単です。
縦と横の合計が0になる
これだけ覚えておきましょう。
明石高専の土木科で構造力学を学んだ僕が日本で1番わかりやすく図解します。
この記事の内容
- 支点反力の求め方は簡単です
- 覚えることは『縦と横に分解して0になる』だけ
- 僕がおススメする参考書もご紹介します
支点反力の求め方をわかりやすく解説します

支点反力を求めるためには、その問題の力を全て絵で描くことが重要です。
力を絵で描く方法は『力のつり合いは絵で描くとわかる【構造力学の基礎】』で詳しく解説しています。まだご覧になってない方はどうぞ。
はりの支点反力を求める基本的な考え方は0になること
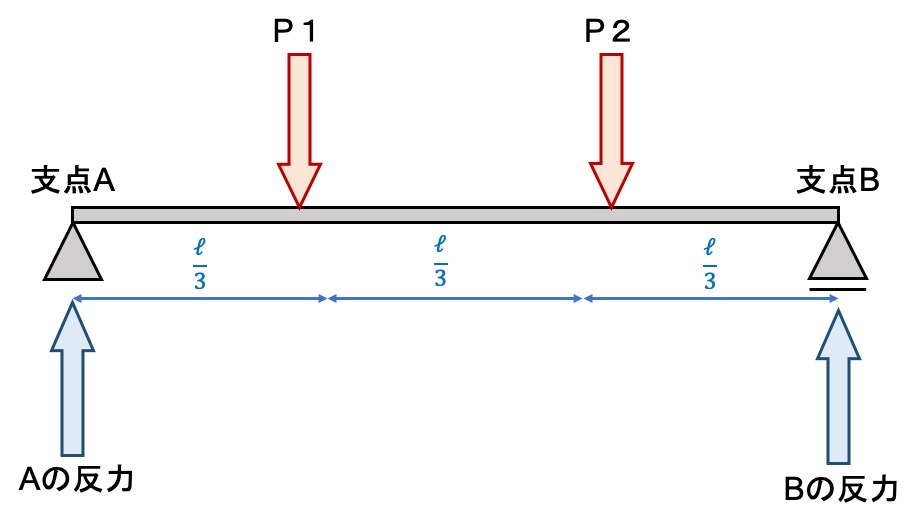
支点反力を求めるために必要なポイントは次の3つです。
- 力を絵で描く
- 縦と横に分ける
- 縦と横それぞれが0になる
力を正しく書く
力のつり合いは絵で描くとわかる【構造力学の基礎】で解説した通りに力を絵で描いてみます。
力を図に正しく書くことができれば、そこから力のつり合いを見つけます。
力のつり合いには次の3つがあります。
- 縦
- 横
- 回転
この3つの力がつり合っているから梁が動きません。
ちなみに、回転は『力の大きさ×距離』で計算できます。
また、梁を支える『支点』には次の3種類があり、それぞれ次の力に抵抗します。
- 固定端:縦・横・回転
- ヒンジ支点:縦・横
- ローラー支点:縦
ぎゅっと握った状態が固定端・ドアの蝶番がヒンジ支点・台車がローラー支点といった感じでしょうか?
力を縦と横に分解する
力を縦と横に分解しましょう。
縦にはV(Vertical)、横にはH(Horizon)を使います。
力の分解には、sin、cos、tanを使って分解します。

三角関数は大切です。
この機会に覚えておきましょう。
| 関数 | 30° | 45° | 60° |
| sin | √3/2 | √2/2 | 1/2 |
| cos | 1/2 | √2/2 | √3/2 |
| tan | √3/3 | 1 | √3 |
例えば、45°の斜め上方向に2kNの力が働いている時、縦と横の力は次のようになります。
- 縦:2kN × cos(45°)=2×(√2/2)=√2
- 横:2kN × sin(45°)=2×(√2/2)=√2

基本的に次のように覚えてください。
縦:cos、横:sin
縦と横と回転のそれぞれの力で方程式を作る
下の画像にあるように力が働いても、物が動かなければ力がつり合っていると言います。
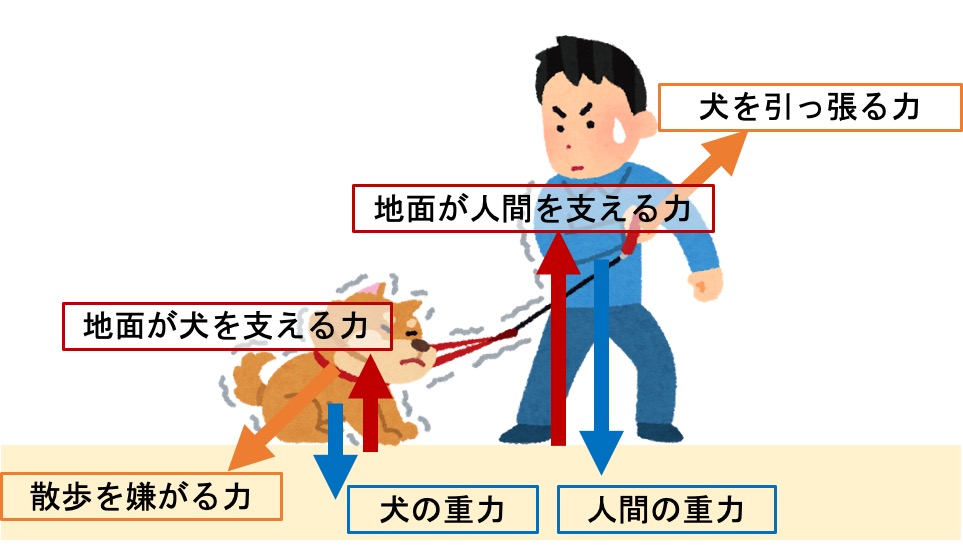
この力のつり合いを利用してはりの支点反力を求めます。
上にあった画像のはりの支点反力を求めてみましょう。
はりの支点反力の求め方:実例
はりにかかる力を具体的に次の数値にします。
1つのはりに5kNと8kNの2つの力が働いています。
この時の支点反力Aと支点反力Bを求めてみましょう。
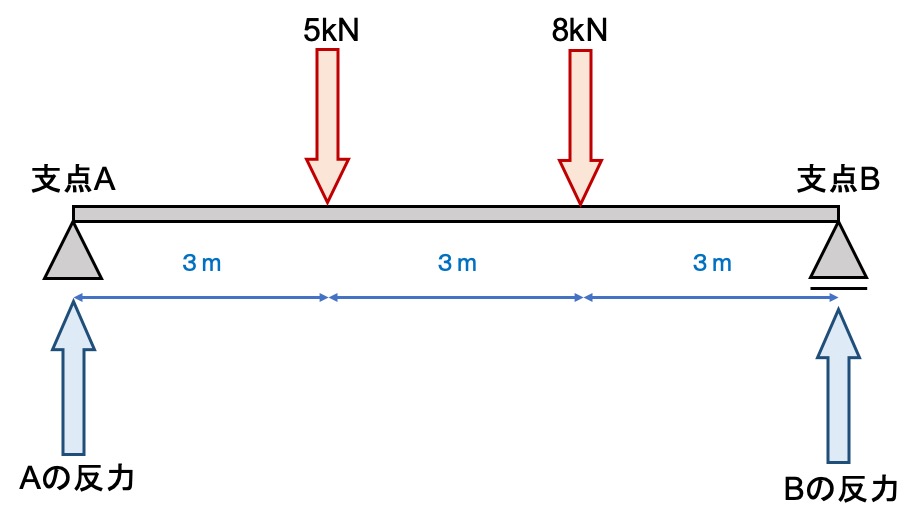
まずは、力を正しく書きましょう。
支点Aはヒンジ支点です。縦と横の力に抵抗しますが、今回は横の力が働いてないので、横の力は0です。
ですので、支点Aの反力は縦方向のみになります。
支点Bはローラー支点です。縦の力に抵抗します。

支点の種類によって、抵抗する力の向きが変わります。
気をつけましょう。
力を縦と横の力に分解しましょう。
今回は斜め方向の力が働いていないので、スキップします。
次に縦と横と回転の力でつり合い式を作りましょう。
横の力は働いていないので以下の式になります。
HA+HB=0
縦の力は下向きに5kNと8kN、上向に支点Aと支点Bの反力なので、以下の式になります。
VA+VB=5kN+8kN

同じ向きの力を同じ辺に入れましょう
回転の力は『力の大きさ×距離』で計算できます。
計算しやすい場所を見つけて、そこからの回転の力を計算してみましょう。

力がいっぱい集まっているところがおすすめです。
なければ、支点Aで計算しましょう。
今回は支点Aを基準にして回転の力を計算してみましょう。
VA ×0m+VB×9m=5kN×3m+8kN×6m

同じ向きに回転する力を同じ辺に入れましょう。
左辺は左回り、右辺は右回りにしています。
力のつり合いの式は以下の式です。
VA+VB=5kN+8kN
VA ×0m+VB×9m=5kN×3m+8kN×6m
これを解くとVAとVBは次のようになります。VA=6kN
VB=7kN
これで、はりの支点反力が求められました。
支点反力の求め方は縦と横に分解するだけ

構造力学で支点反力を求めることは、今後の断面力や影響線を求める基本になります。
この機会にマスターしておきましょう。
構造力学が苦手だなー...と思うあなたのために、こちらの『【土木】構造力学の参考書はこれがおすすめ』でテストで点数が取れる参考書を紹介しています。
構造力学は多く問題を解けばマスターできます。参考書を使いながら勉強して行きましょう。

